【题目】如图,点E、F、G、H分别在菱形ABCD的四条边上,BE=BF=DG=DH,连接EF,FG,GH,HE,得到四边形EFGH,若AB=a,∠A=60°,当四边形
EFGH的面积取得最大时,BE的长度为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】C
【解析】
试题分析:利用等腰三角形的性质:等边对等角,以及平行线的性质可以证得∠DGH+∠CGH=90°,则∠HGF=90°,根据三个角是直角的四边形是矩形,可证得四边形EFGH是矩形;设BE的长是x,则利用x表示出矩形EFGH的面积,根据函数的性质即可求解.
解:∵DG=DH,
∴∠DHG=∠DGH,
同理∠CGF=![]() ,
,
∴∠DGH+∠CGF=![]() ,
,
又∵菱形ABCD中,AD∥BC,
∴∠D+∠C=180°,
∴∠DGH+∠CGF=90°,
∴∠HGF=90°,
同理,∠GHE=90°,∠EFG=90°,
∴四边形EFGH是矩形;
∵AB=a,∠A=60°,
∴菱形ABCD的面积是:![]() a2,
a2,
设BE=x,则AE=a﹣x,
则△AEH的面积是:![]() ,
,
△BEF的面积是:![]() ,
,
则矩形EFGH的面积y=![]() a2﹣
a2﹣![]() ﹣
﹣![]() x2,
x2,
即y=﹣![]() x2+
x2+![]() ax,
ax,
则当x=![]() =
=![]() 时,函数有最大值.
时,函数有最大值.
此时BE=![]() .
.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】DNA分子的直径只有0.000 000 2 cm,将0.000 000 2用科学记数法表示为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+2x+a﹣2=0.
(1)若该方程有两个不相等的实数根,求实数a的取值范围;
(2)设方程两根为x1,x2是否存在实数a,使
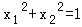 ?若存在求出实数a,若不存在,请说明理由.
?若存在求出实数a,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中不正确的是( )
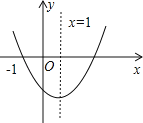
A.ac<0
B.b<0
C.b2﹣4ac<0
D.x=3关于x方程ax2+bx+c=0一个根
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下列方程:
(1)(2x+1)2=(x﹣1)2
(2)
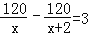 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(2x-1)(5x+2)等于( )
A. 10x2-2 B. 10x2-x-2 C. 10x2+4x-2 D. 10x2-5x-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块长方形区域,而且这三块长方形区域的面积相等.设BC的长度为xm,AB为ym.

(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)当BC为多长时,长方形面积达300m2?
相关试题

