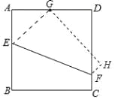
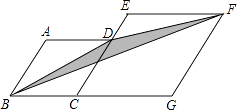
【题目】如图,将边长为4的正方形ABCD沿着折痕EF折叠,使点B落在边AD的中点G处.
(1)求线段BE的长;
(2)连接BF、GF,求证:BF=GF;
(3)求四边形BCFE的面积.
参考答案:
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)由折叠的性质可得![]() ,
,![]() ,设
,设![]() ,则
,则![]() ,在
,在![]() 中利用勾股定理求出
中利用勾股定理求出![]() 的值;
的值;
(2)根据折叠的性质即可求解;
(3)四边形![]() 是梯形,要求其面积需要得出
是梯形,要求其面积需要得出![]() 的长,可通过求出
的长,可通过求出![]() 的长度,进行求解.
的长度,进行求解.
(1)由题意,点![]() 与点
与点![]() ,点
,点![]() 与点
与点![]() 分别关于直线
分别关于直线![]() 对称,
对称,
![]()
![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() 落在边
落在边![]() 的中点
的中点![]() 处,
处,
![]()
![]() ,
,
![]()
![]() ,
,
解得:![]() ,
,
![]()
![]() .
.
(2)![]() 将边长为
将边长为![]() 的正方形
的正方形![]() 沿着折痕
沿着折痕![]() 折叠,使点
折叠,使点![]() 落在边
落在边![]() 的中点
的中点![]() 处,连接BF、GF,在△BFE和△GFE中,BE=GE,∠BEF=∠GEF,EF=EF,∴△BFE≌△GFE
处,连接BF、GF,在△BFE和△GFE中,BE=GE,∠BEF=∠GEF,EF=EF,∴△BFE≌△GFE
![]()
![]() ;
;
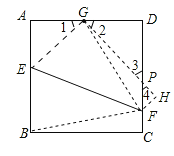
(3)
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]()
![]() ,
,![]() ,
,
![]() 点
点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上,
边上,
![]() 四边形
四边形![]() 是直角梯形,
是直角梯形,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
在![]() 中,
中,![]()
![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
在![]() 中,
中,![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论有( )

A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
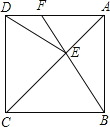
查看答案和解析>>【题目】如图,在一方形ABCD中.E为对角线AC上一点,连接EB、ED,
(1)求证:△BEC≌△DEC:
(2)延长BE交AD于点F,若∠DEB=140°.求∠AFE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某手机店今年1-4月的手机销售总额如图1,其中一款音乐手机的销售额占当月手机销售总额的百分比如图2.有以下四个结论:
①从1月到4月,手机销售总额连续下降
②从1月到4月,音乐手机销售额在当月手机销售总额中的占比连续下降
③音乐手机4月份的销售额比3月份有所下降
④今年1-4月中,音乐手机销售额最低的是3月
其中正确的结论是________(填写序号).

-
科目: 来源: 题型:
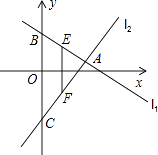
查看答案和解析>>【题目】如图,已知直线l1:y=k1x+4与直线l2:y=k2x﹣5交于点A,它们与y轴的交点分别为点B,C,点E,F分别为线段AB、AC的中点,则线段EF的长度为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=1,点P是BC边上的任意一点(异于端点B、C),连接AP,过B、D两点作BE⊥AP于点E,DF⊥AP于点F.
(1)求证:EF=DF﹣BE;
(2)若△ADF的周长为
 ,求EF的长.
,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD和菱形ECGF的边长分别为2和4,∠A=120°.则阴影部分面积是 . (结果保留根号)
相关试题

