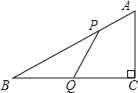
【题目】如图,在△ABC中,∠C=90°,AB=10,BC=8,P、Q分别是AB、BC边上的点,且AP=BQ=a (其中0<a<8).
(1)若PQ⊥BC,求a的值;
(2)若PQ=BQ,把线段CQ绕着点Q旋转180°,试判别点C的对应点C’是否落在线段QB上?请说明理由.
参考答案:
【答案】(1)![]() (2)点C′不落在线段QB上
(2)点C′不落在线段QB上
【解析】试题分析: (1)∵∠B=∠B,∠PQB=∠C=90°∴△BQP∽△BCA,
∴![]() ,
,![]() ,解得:a=
,解得:a=![]() ,
,
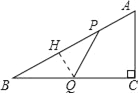
(2) 作QH⊥AB于H,∵PQ=BQ,∴BH=HP,∵∠B=∠B,∠BHQ=∠C,∴△BQH∽△BAC,
∴BH:BC=BQ:AB可得: ![]() (10﹣a):a=8:10,解得a=
(10﹣a):a=8:10,解得a=![]() ,CQ=(8﹣a)=
,CQ=(8﹣a)=![]() ,
,
∴BQ<QC,∴点C′不落在线段QB上.
试题解析:(1)∵∠B=∠B,∠PQB=∠C=90°
∴△BQP∽△BCA,
∴![]() ,
,![]() ,
,
解得:a=![]() ,
,
(2)点C′不落在线段QB上,
作QH⊥AB于H,
∵PQ=BQ,
∴BH=HP,
∵∠B=∠B,∠BHQ=∠C,
∴△BQH∽△BAC,
∴BH:BC=BQ:AB可得: ![]() (10﹣a):a=8:10,
(10﹣a):a=8:10,
解得a=![]() ,
,
CQ=(8﹣a)=![]() ,
,
∴BQ<QC,
∴点C′不落在线段QB上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=
 ,且使y=k成立的x值恰好有2个,则k的取值范是_____.
,且使y=k成立的x值恰好有2个,则k的取值范是_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 为
为 的中点,
的中点, ,
, .动点
.动点 从点
从点 出发,沿
出发,沿 方向以
方向以 的速度向点
的速度向点 运动;同时动点
运动;同时动点 从点
从点 出发,沿
出发,沿 方向以
方向以 的速度向点
的速度向点 运动,运动时间是
运动,运动时间是 秒.
秒.
(1)用含
 的代数式表示
的代数式表示 的长度.
的长度.(2)在运动过程中,是否存在某一时刻
 ,使点
,使点 位于线段
位于线段 的垂直平分线上?若存在,求出
的垂直平分线上?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(3)是否存在某一时刻
 ,使
,使 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(4)是否存在某一时刻
 ,使
,使 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
(1)如图①,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为 .
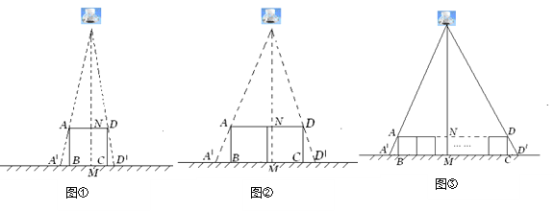 (2)不改变①中灯泡的高度,将两个边长为30cm的正方形框架按图②摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(2)不改变①中灯泡的高度,将两个边长为30cm的正方形框架按图②摆放,请计算此时横向影子A′B,D′C的长度和为多少?(3)有n个边长为a的正方形按图③摆放,测得横向影子A′B,D′C的长度和为b,求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,要说明△ABD≌△ACD,还需从下列条件中选一个,错误的选法是( )
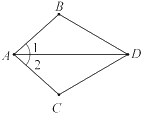
A. ∠ADB=∠ADCB. ∠B=∠CC. DB=DCD. AB=AC
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,甲地到乙地的路程为450千米,一辆大货车从甲地前往乙地运送物资,行驶1小时在途中某地出现故障,立即通知技术人员乘小汽车从甲地赶来维修(通知时间忽略不计),小汽车到达该地后经过半小时修好大货年后以原速原路返甲地,小汽车在返程途中当走到一半路程时发现有重要物品落在大货车上,于是立即掉头以原速追赶大货车,追上大货车取下物品(取物品时间忽略不计)后以原速原路返回甲地,大货车修好后以原速前往乙地,如图是两车距甲地的路程y(千米)与大货车所用时间x(小时)之间的函数图象,则当小汽车第二次追上大货车时,大货车距离乙地_____千米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B
 C
C D作匀速运动,那么△ABP的面积
D作匀速运动,那么△ABP的面积 与点P运动的路程之间的函数图象大致是( ).
与点P运动的路程之间的函数图象大致是( ).
A.
 B.
B.  C.
C.  D.
D. 
相关试题

