【题目】某商场销售两款三星的智能手机,这两款手机的进价和售价如下表所示:

该商场计划购进两款手机若干部,共需15.5万元,预计全部销售后获毛利润共2.1万元(毛利润=(售价-进价)×销售量)
(1)该商场计划购进甲、乙两款手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲手机的购进数量,增加乙手机的购进数量,已知乙手机增加的数量是甲手机减少的数量的3倍,而且用于购进这两款手机的总资金不超过17.25万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润。
参考答案:
【答案】(1)该商场计划购进甲种手机20部,乙种手机30部;(2)当商场购进甲种手机15部,乙种手机45部时,全部销售后毛利润最大,最大毛利润是2.7万元.
【解析】
试题分析:(1)设商场计划购进甲种手机x部,乙种手机y部,根据两种手机的购买金额为15.5万元和两种手机的销售利润为2.1万元建立方程组求出其解即可;
(2)设甲种手机减少a部,则乙种手机增加2a部,表示出购买的总资金,由总资金不超过17.25万元建立不等式就可以求出a的取值范围,再设销售后的总利润为W元,表示出总利润与a的关系式,由一次函数的性质就可以求出最大利润.
试题解析:(1)设该商场计划购进甲种手机x部,乙种手机y部,由题意得
![]() ,
,
解得![]() .
.
答:该商场计划购进甲种手机20部,乙种手机30部;
(2)设甲种手机减少a部,则乙种手机增加3a部,由题意得4000(20-a)+2500(30+3a)≤172500
解得a≤5
设全部销售后的毛利润为w元.则
w=300(20-a)+500(30+3a)=1200a+21000.
∵1200>0,
∴w随着a的增大而增大,
∴当a=5时,w有最大值,w最大=1200×5+21000=27000
答:当商场购进甲种手机15部,乙种手机45部时,全部销售后毛利润最大,最大毛利润是2.7万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正n边形的内角和等于900°,则n= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式3x2y﹣xy3+5xy﹣1是一个( )
A. 四次三项式 B. 三次三项式 C. 四次四项式 D. 三次四项式
-
科目: 来源: 题型:
查看答案和解析>>【题目】∠α的补角比∠α的余角的3倍大10°,则∠α=__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某区八年级学生身体素质情况,该区从全区八年级学生中随机抽取了部分学生进行了一次体育考试科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
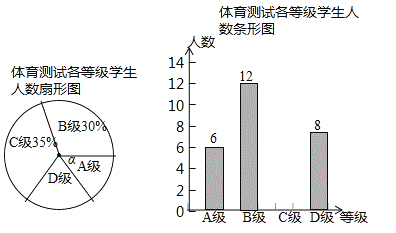
(1)本次抽样测试的学生人数是 ;
(2)图1中∠α的度数是 ;4并把图2条形统计图补充完整;
(3)该区八年级有学生3500名,如果全部参加这次体育科目测试,请估计不及格的人数为 ;
(4)测试老师想从4位同学(分别记为E、F、G、H,其中E为小明)中随机选择两位同学了解平时训练情况,请用列表或画树形图的方法求出选中小明的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
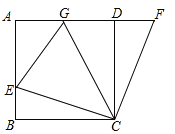
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为提倡节约用水,采取分段收费.若每户每月用水量不超过20 m3,每立方米收费2元;若用水量超过20 m3,超过部分每立方米加收1元.小明家5月份交水费64元,则他家该月用水________.
相关试题

