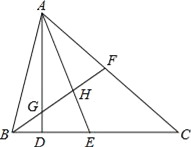
【题目】如图:(1)AD⊥BC,垂足为D,则AD是__的高,∠__=∠__=90°;
(2)AE平分∠BAC,交BC于点E,则AE叫__,∠__=∠__=![]() ∠__,AH叫__;
∠__,AH叫__;
(3)若AF=FC,则△ABC的中线是__;
(4)若BG=GH=HF,则AG是__的中线,AH是__的中线.
参考答案:
【答案】 BC边上 ADB ADC ∠BAC的角平分线 BAE CAE BAC ∠BAF的角平分线 BF △ABH △AGF
【解析】试题解析:(1)AD⊥BC,垂足为D,则AD是BC边上的高, ![]()
(2)AE平分∠BAC,交BC于点E,则AE叫∠BAC的角平分线, ![]() AH叫∠BAF的角平分线;
AH叫∠BAF的角平分线;
(3)若AF=FC,则△ABC的中线是BF;
(4)若BG=GH=HF,则AG是△ABH的中线,AH是△AGF的中线。
故答案为(1)BC边上,ADB,ADC;(2)∠BAC的角平分线,BAE,CAE,BAC,∠BAF的角平分线;(3)BF;(4)△ABH,△AGF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在图(1)中,A1、B1、C1分别是△ABC的边BC、CA、AB的中点,在图(2)中,A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点,…,按此规律,则第n个图形中平行四边形的个数共有个

-
科目: 来源: 题型:
查看答案和解析>>【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,
求证:四边形ABCD是四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇的想法写出证明;
(3)用文字叙述所证命题的逆命题为平行四边形两组对边分别相等 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=________,若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M=__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】聊城“水城之眼”摩天轮是亚洲三大摩天轮之一,也是全球首座建筑与摩天轮相结合的城市地标,如图,点O是摩天轮的圆心,长为110米的AB是其垂直地面的直径,小莹在地面C点处利用测角仪测得摩天轮的最高点A的仰角为33°,测得圆心O的仰角为21°,则小莹所在C点到直径AB所在直线的距离约为(tan33°≈0.65,tan21°≈0.38)( )

A.169米 B.204米 C.240米 D.407米
-
科目: 来源: 题型:
查看答案和解析>>【题目】求下列各式中x的值:
(1)2x2-32=0;
(2)(x+4)3+64=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
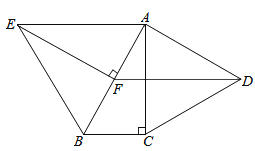
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
相关试题

