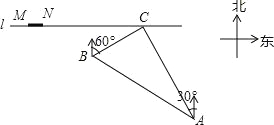
【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.以轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由.(参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
参考答案:
【答案】(1)轮船照此速度与航向航向,上午11::00到达海岸线;(2)轮船不改变航向,轮船可以停靠在码头,理由详见解析.
【解析】
试题分析:(1)延长AB交海岸线l于点D,过点B作BE⊥海岸线l于点E,过点A作AF⊥l于F,易证△ABC是直角三角形,再证明∠BAC=30°,再求出BD的长即可解决问题.(2)在RT△BEC中,求出CD的长度,和CN、CM比较即可解决问题.
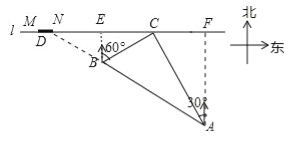
试题解析:(1)延长AB交海岸线l于点D,过点B作BE⊥海岸线l于点E,过点A作AF⊥l于F,如图所示.
∵∠BEC=∠AFC=90°,∠EBC=60°,∠CAF=30°,
∴∠ECB=30°,∠ACF=60°,
∴∠BCA=90°,
∵BC=12,AB=36×![]() =24,
=24,
∴AB=2BC,
∴∠BAC=30°,∠ABC=60°,
∵∠ABC=∠BDC+∠BCD=60°,
∴∠BDC=∠BCD=30°,
∴BD=BC=12,
∴时间t=![]() =
=![]() 小时=20分钟,
小时=20分钟,
∴轮船照此速度与航向航向,上午11::00到达海岸线.
(2)∵BD=BC,BE⊥CD,
∴DE=EC,
在RT△BEC中,∵BC=12,∠BCE=30°,
∴BE=6,EC=6![]() ≈10.2,
≈10.2,
∴CD=20.4,
∵20<20.4<21.5,
∴轮船不改变航向,轮船可以停靠在码头.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若三条直线交于一点,则共有对顶角(平角除外) ( )
A.6对B.5对C.4对D.3对
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知ABCD的三个顶点坐标分别是A(m,n),B(2,-1),C(-m,-n),则点D的坐标是( )
A.(-2,1)
B.(-2,-1)
C.(-1,-2)
D.(-1,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】清朝康熙皇帝是我国历史上对数学很有兴趣的帝王近日,西安发现了他的数学专著,其中有一文《积求勾股法》,它对“三边长为3、4、5的整数倍的直角三角形,已知面积求边长”这一问题提出了解法:“若所设者为积数(面积),以积率六除之,平方开之得数,再以勾股弦各率乘之,即得勾股弦之数”.用现在的数学语言表述是:“若直角三角形的三边长分别为3、4、5的整数倍,设其面积为S,则第一步:
 =m;第二步:
=m;第二步:  =k;第三步:分别用3、4、5乘以k,得三边长”.
=k;第三步:分别用3、4、5乘以k,得三边长”.(1)当面积S等于150时,请用康熙的“积求勾股法”求出这个直角三角形的三边长;
(2)你能证明“积求勾股法”的正确性吗?请写出证明过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正多边形的每个外角都是36°,这个正多边形的边数是
-
科目: 来源: 题型:
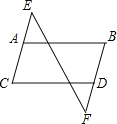
查看答案和解析>>【题目】如图,现有以下3句话:①AB∥CD,②∠B=∠C.③∠E=∠F.请以其中2句话为条件,第三句话为结论构造命题.例如:由①②得③.
(1)你还能构造几个命题?请仿照上面的例子,将它们写出来.
(2)你构所造的命题是真命题还是假命题?请选择一个加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们可以把“火车在一段笔直的铁轨上行驶了一段距离”看作“火车沿铁轨方向_________”.
相关试题

