【题目】如图,抛物线y=ax2+bx+c经过A(﹣ ![]() ,0)、B(3
,0)、B(3 ![]() ,0)、C(0,3)三点,线段BC与抛物线的对称轴相交于D.该抛物线的顶点为P,连接PA、AD、DP,线段AD与y轴相交于点E.
,0)、C(0,3)三点,线段BC与抛物线的对称轴相交于D.该抛物线的顶点为P,连接PA、AD、DP,线段AD与y轴相交于点E. 
(1)求该抛物线的解析式;
(2)在平面直角坐标系中是否存在点Q,使以Q、C、D为顶点的三角形与△ADP全等?若存在,求出点Q的坐标;若不存在,说明理由;
(3)将∠CED绕点E顺时针旋转,边EC旋转后与线段BC相交于点M,边ED旋转后与对称轴相交于点N,连接PM、DN,若PM=2DN,求点N的坐标(直接写出结果).
参考答案:
【答案】
(1)
解:设抛物线的解析式为:y=a(x+ ![]() )(x﹣3
)(x﹣3 ![]() ),代入点C(0,3)后,得:
),代入点C(0,3)后,得:
a(0+ ![]() )(0﹣3
)(0﹣3 ![]() )=3,解得 a=﹣
)=3,解得 a=﹣ ![]()
∴抛物线的解析式:y=﹣ ![]() (x+
(x+ ![]() )(x﹣3
)(x﹣3 ![]() )=﹣
)=﹣ ![]() x2+
x2+ ![]() x+3
x+3
(2)
解:设直线BC的解析式:y=kx+b,依题意,有:
![]() ,
,
解得 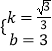 .
.
故直线BC:y=﹣ ![]() x+3.
x+3.
由抛物线的解析式知:P( ![]() ,4),将点P的横坐标代入直线BC中,得:D(
,4),将点P的横坐标代入直线BC中,得:D( ![]() ,2).
,2).
设点Q(x,y),则有:
QC2=(x﹣0)2+(y﹣3)2=x2+y2﹣6y+9、QD2=(x﹣ ![]() )2+(y﹣2)2=x2+y2﹣2
)2+(y﹣2)2=x2+y2﹣2 ![]() x﹣4y+7;
x﹣4y+7;
而:PA2=(﹣ ![]() ﹣
﹣ ![]() )2+(0﹣4)2=28、AD2=(﹣
)2+(0﹣4)2=28、AD2=(﹣ ![]() ﹣
﹣ ![]() )2+(0﹣2)2=16、CD=PD=2;
)2+(0﹣2)2=16、CD=PD=2;
△QCD和△APD中,CD=PD,若两个三角形全等,则:
①QC=AP、QD=AD时, ![]()
②QC=AD、QD=AP时, ![]()
解①、②的方程组,得: ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() ;
;
∴点Q的坐标为(3 ![]() ,4)、(
,4)、( ![]() ,﹣2)、(﹣2
,﹣2)、(﹣2 ![]() ,1)或(0,7)
,1)或(0,7)
(3)
解:根据题意作图如右图;

由D( ![]() ,2)、B(3
,2)、B(3 ![]() ,0)知:DF=2,BF=2
,0)知:DF=2,BF=2 ![]() ;
;
∴∠BDF=∠ADF=∠CDE=∠DCE=60°,即△CED是等边三角形;
在△CEM和△DEN中, 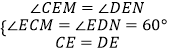
∴△CEM≌△DEN,则 CM=DN,PM=2CM=2DN;
设点M(x,﹣ ![]() x+3),则有:
x+3),则有:
PM2=( ![]() ﹣x)2+(4+
﹣x)2+(4+ ![]() x﹣3)2=
x﹣3)2= ![]() x2﹣
x2﹣ ![]()
![]() x+4、CM2=x2+
x+4、CM2=x2+ ![]() x2=
x2= ![]() x2;
x2;
已知:PM2=4CM2,则有:
![]() x2﹣
x2﹣ ![]()
![]() x+4=4×
x+4=4× ![]() x2,解得 x=
x2,解得 x= ![]() ;
;
∴CM=DN= ![]() ×x=
×x= ![]() ×
× ![]() =
= ![]() ;
;
则:FN=DF﹣DN=2﹣ ![]() =
= ![]() ,
,
∴点N( ![]() ,
, ![]() ).
).
【解析】(1)已知抛物线经过的三点坐标,直接利用待定系数法求解即可.(2)由于点Q的位置可能有四处,所以利用几何法求解较为复杂,所以可考虑直接用SSS判定两三角形全等的方法来求解.那么,首先要证明CD=DP,设出点Q的坐标后,表示出QC、QD的长,然后由另两组对应边相等列方程来确定点Q的坐标.(3)根据B、D的坐标,容易判断出△CDE是等边三角形,然后通过证△CEM、△DEN全等来得出CM=DN,首先设出点M的坐标,表示出PM、CM的长,由PM=2DN=2CM列方程确定点M的坐标,进一步得到CM的长后,即可得出DN的长,由此求得点N的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校初二年级数学考试,(满分为100分,该班学生成绩均不低于50分)作了统计分析,绘制成如图频数分布直方图和频数、频率分布表,请你根据图表提供的信息,解答下列问题:
分组
49.5~59.5
59.5~69.5
69.5~79.5
79.5~89.5
89.5~100.5
合计
频数
2
a
20
16
4
50
频率
0.04
0.16
0.40
0.32
b
1

(1)频数、频率分布表中a= ,b= ;(答案直接填在题中横线上)
(2)补全频数分布直方图;
(3)若该校八年级共有600名学生,且各个班级学生成绩分布基本相同,请估计该校八年级上学期期末考试成绩低于70分的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形ABCD中,AD∥BC,∠ABC=2∠BCD=2α,点E在AD上,点F在DC上,且∠BEF=∠A.

(1)∠BEF=(用含α的代数式表示);
(2)当AB=AD时,猜想线段EB、EF的数量关系,并证明你的猜想;
(3)当AB≠AD时,将“点E在AD上”改为“点E在AD的延长线上,且AE>AB,AB=mDE,AD=nDE”,其他条件不变(如图),求 的值(用含m,n的代数式表示)
的值(用含m,n的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】把三角形按如图所示的规律拼图案,其中第①个图案中有4个三角形,第②个图案中有6个三角形,第③个图案中有8个三角形,…,按此规律排列下去,则第⑦个图案中三角形的个数为( )
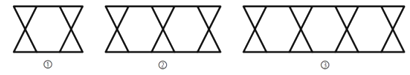
A. 12 B. 14 C. 16 D. 18
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着-5,-2,1,9,且任意相邻四个台阶上数的和都相等.
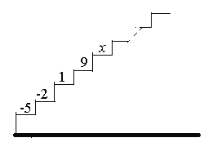
(1)求前4个台阶上数的和是多少?
(2)求第5个台阶上的数
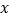 是多少?
是多少?(3)从下到上前多少个台阶上数的和为30.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如上图,正方形网格中的每个小正方形边长都是1,任意连接这些小正方形的顶点,可得到一些线段;请在图中画出AB=
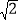 ,CD=
,CD=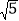 ,EF=
,EF=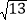 这样的线段;
这样的线段;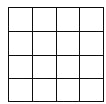
(2)如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°后的图形△ABC;并计算对应点B和B之间的距离?
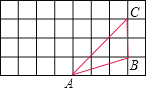
(3)如图是由5个边长为1的小正方形拼成的.
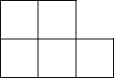
①将该图形分成三块(在图中画出),使由这三块可拼成一个正方形;
②求出所拼成的正方形的面积S.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点M,O,N对应的数分别为-1,0,3,点P为数轴上任意一点,其对应的数为x.

(1)MN的长为 ;
(2)如果点P到点M、点N的距离相等,那么x的值是 ;
(3)数轴上是否存在点P,使点P到点M、点N的距离之和是8?若存在,直接写出x的值;若不存在,请说明理由.
(4)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
相关试题

