【题目】放风筝是大家喜爱的一种运动.星期天的上午小明在大洲广场上放风筝.如图他在A处时不小心让风筝挂在了一棵树的树梢上,风筝固定在了D处.此时风筝线AD与水平线的夹角为30°. 为了便于观察.小明迅速向前边移动边收线到达了离A处7米的B处,此时风筝线BD与水平线的夹角为45°.已知点A、B、C在冋一条直线上,∠ACD=90°.请你求出小明此吋所收回的风筝线的长度是多少米?(本题中风筝线均视为线段, ![]() ≈1.414,
≈1.414, ![]() ≈1.732.最后结果精确到1米)
≈1.732.最后结果精确到1米)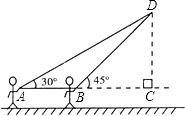
参考答案:
【答案】解:设CD为x米.
∵∠ACD=90°,
∴在直角△ADC中,∠DAC=30°,AC=CD÷tan30°= ![]() x,
x,
在直角△BCD中,∠DBC=45°,BC=CD=x,BD= ![]() x,
x,
∵AC﹣BC=AB=7米,
∴ ![]() x﹣x=7,
x﹣x=7,
又∵ ![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732,
∴x=10米,
则小明此时所收回的风筝的长度为:AD﹣BD=2x﹣ ![]() x≈6(米)
x≈6(米)
【解析】设CD为x米,根据三角函数即可表示出AC于BC的长,根据AC﹣BC=AB即可得到一个关于x的方程,解方程即可求得x的值.
【考点精析】掌握锐角三角函数的定义和特殊角的三角函数值是解答本题的根本,需要知道锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数;分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】营市公交公司将淘汰所有线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1220万元,且确保这10辆公交车在该线路的年均载客总和不少于650万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小英和小明姐弟二人准备一起去观看端午节龙舟赛.但因家中临时有事,必须留下一人在家,于是姐弟二人采用游戏的方式来确定谁去看龙舟赛.游戏规则是:在不透明的口袋中分别放入2个白色和1个黄色的乒乓球,它们除颜色外其余都相同.游戏时先由小英从口袋中任意摸出1个乒乓球记下颜色后放回并摇匀,再由小明从口袋中摸出1个乒乓球,记下颜色.如果姐弟二人摸到的乒乓球颜色相同.则小英赢,否则小明赢.
(1)请用树状图或列表的方法表示游戏中所有可能出现的结果.
(2)这个游戏对游戏双方公平吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】按下列程序进行运算(如图)
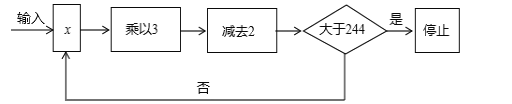
规定:程序运行到“判断结果是否大于244”为一次运算,若运算进行了5次才停止,则x的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正比例函数y1=k1x与反比例函数y2=
 相交于A、B点.已知点A的坐标为A(4,n),BD⊥x轴于点D,且S△BDO=4.过点A的一次函数y3=k3x+b与反比例函数的图象交于另一点C,与x轴交于点E(5,0).
相交于A、B点.已知点A的坐标为A(4,n),BD⊥x轴于点D,且S△BDO=4.过点A的一次函数y3=k3x+b与反比例函数的图象交于另一点C,与x轴交于点E(5,0). 
(1)求正比例函数y1、反比例函数y2和一次函数y3的解析式;
(2)结合图象,求出当k3x+b> >k1x时x的取值范围.
>k1x时x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】“400人中有两人的生日在同一天”这个事件是( )
A.必然事件B.随机事件C.不可能事件D.都不是
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. x6+x6=2x12B. a2a4﹣(﹣a3)2=0
C. (x﹣y)2=x2﹣2xy﹣y2D. (a+b)(b﹣a)=a2+b2
相关试题

