【题目】在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5 ![]() 千米的C处.
千米的C处.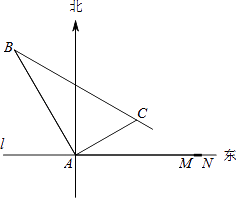
(1)该飞机航行的速度是多少千米/小时?(结果保留根号)
(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由.
参考答案:
【答案】
(1)
解:由题意,得∠BAC=90°,
∴BC= ![]() =10
=10 ![]() ,
,
∴飞机航行的速度为:10 ![]() ×60=600
×60=600 ![]() (km/h)
(km/h)
(2)
解:能;
作CE⊥l于点E,设直线BC交l于点F.
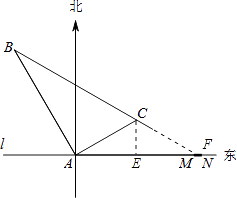
在Rt△ABC中,AC=5 ![]() ,BC=10
,BC=10 ![]() ,
,
∴∠ABC=30°,即∠BCA=60°,
又∵∠CAE=30°,∠ACE=∠FCE=60°,
∴CE=ACsin∠CAE= ![]() ,
,
AE=ACcos∠CAE= ![]() .
.
则AF=2AE=15(km),
∴AN=AM+MN=14.5+1=15.5km,
∵AM<AF<AN,
∴飞机不改变航向继续航行,可以落在跑道MN之间.
【解析】(1)先求出∠BAC=90°,然后利用勾股定理列式求解即可得到BC,再求解即可;(2)作CE⊥l于E,设直线BC交l于F,然后求出CE、AE,然后求出AF的长,再进行判断即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以lcm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为l,设运动时间为t秒.
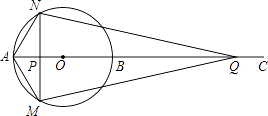
(1)若AC=5,则当t=时,四边形AMQN为菱形;当t=时,NQ与⊙O相切;
(2)当AC的长为多少时,存在t的值,使四边形AMQN为正方形?请说明理由,并求出此时t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践
问题情境:在棱长为1的正方体右侧拼搭若干个棱长小于或等于1的其它正方体,使拼成的立体图形为一个长方体.如图1,是两个棱长为1的正方体搭成的长方体,图2是从上面看这个长方体得到的平面图形,它由两个正方形组成.

操作探究:
(1)如图3是在棱长为1的正方体右侧拼搭了4个棱长小于1的正方体形成的长方体,请画出从上面看这个长方体得到的平面图形;
(2)已知一个长方体是按上述方式拼成的,组成它的正方体不超过10个,且若从上面看这个长方体得到的平面图形由4个正方形组成.
请从A,B两题中任选一题作答,我选择 题.
A.请画出从上面看这个长方体得到的平面图形.(请画出所有可能的图形)
B.请画出从上面看这个长方体得到的平面图形.(请画出所有可能的图形,并在所画图形的下方直接写出拼成该长方体所需的正方体的总个数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
阅读材料:
数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.例如,两个有理数在数轴上对应的点之间的距离可以用这两个数的差的绝对值表示;
在数轴上,有理数3与1对应的两点之间的距离为|3﹣1|=2;
在数轴上,有理数5与﹣2对应的两点之间的距离为|5﹣(﹣2)|=7;
在数轴上,有理数﹣2与3对应的两点之间的距离为|﹣2﹣3|=5;
在数轴上,有理数﹣8与﹣5对应的两点之间的距离为|﹣8﹣(﹣5)|=3;……
如图1,在数轴上有理数a对应的点为点A,有理数b对应的点为点B,A,B两点之间的距离表示为|a﹣b|或|b﹣a|,记为|AB|=|a﹣b|=|b﹣a|.

解决问题:
(1)数轴上有理数﹣10与﹣5对应的两点之间的距离等于 ;数轴上有理数x与﹣5对应的两点之间的距离用含x的式子表示为 ;若数轴上有理数x与﹣1对应的两点A,B之间的距离|AB|=2,则x等于 ;
联系拓广:
(2)如图2,点M,N,P是数轴上的三点,点M表示的数为4,点N表示的数为﹣2,动点P表示的数为x.
请从A,B两题中任选一题作答,我选择 题.
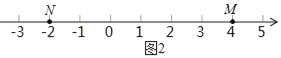
A.①若点P在点M,N两点之间,则|PM|+|PN|= ;
②若|PM|=2|PN|,即点P到点M的距离等于点P到点N的距离的2倍,则x等于 .
B.①若点P在点M,N之间,则|x+2|+|x﹣4|= ;
若|x+2|+|x﹣4|═10,则x= ;
②根据阅读材料及上述各题的解答方法,|x+2|+|x|+|x﹣2|+|x﹣4|的最小值等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,四边形OABC是正方形,点A,C的坐标分别为(2,0),(0,2),D是x轴正半轴上的一点(点D在点A的右边),以BD为边向外作正方形BDEF(E,F两点在第一象限),连接FC交AB的延长线于点G.若反比例函数
 的图象经过点E,G两点,则k的值为 ______________.
的图象经过点E,G两点,则k的值为 ______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.

(1)【发现证明】
小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
(2)【类比引申】
如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足关系时,仍有EF=BE+FD.
(3)【探究应用】
如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40( ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:  =1.41,
=1.41,  =1.73)
=1.73)
相关试题

