【题目】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AC于E,交AD于F,FG∥BC,FH∥AC,下列结论:①AE=AF;②AF=FH;③AG=CE;④AB+FG=BC,其中正确的结论有 . (填序号)
参考答案:
【答案】①②③④
【解析】①正确.
∵∠BAC=90°
∴∠ABE+∠AEB=90°
∴∠ABE=90°-∠AEB
∵AD⊥BC
∴∠ADB=90°
∴∠DBE+∠BFD=90°
∴∠DBE=90-∠BFD
∵∠BFD=∠AFE
∴∠DBE=90°-∠AFE
∵BE平分∠ABC
∴∠ABE=∠DBE
∴90°-∠AEB=90°-∠AFE
∴∠AEB=∠AFE
∴AE=AF
②正确.
∵∠BAC=90°
∴∠BAF+∠DAC=90°
∴∠BAF=90°-∠DAC
∵AD⊥BC
∴∠ADC=90°
∴∠C+∠DAC=90°
∴∠C=90°-∠DAC
∴∠C=∠BAF
∵FH∥AC
∴∠C=∠BHF
∴∠BAF=∠BHF
在△ABF和△HBF中
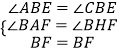
∴△ABF≌△HBF
∴AF=FH
③正确.
∵AE=AF,AF=FH
∴AE=FH
∵FG∥BC,FH∥AC
∴四边形FHCG是平行四边形
∴FH=GC
∴AE=GC
∴AE+EG=GC+EG
∴AG=CE
④正确.
∵四边形FHCG是平行四边形
∴FG=HC
∵△ABF≌△HBF
∴AB=HB
∴AB+FG=HB+HC=BC
故正确的答案有①②③④.
①根据直角三角形两锐角互余得出∠ABE=90°-∠AEB ,∠DBE=90-∠BFD ,根据对顶角相等及等量代换得出∠DBE=90°-∠AFE ,根据角平分线的定义得出∠ABE=∠DBE ,从而得出∠AEB=∠AFE ,根据等边对等角得出AE=AF ; ② 根据垂直的定义得出∠BAF=90°-∠DAC ,根据直角三角形两锐角互余得出∠C=90°-∠DAC ,根据同角的余角相等得出∠C=∠BAF ,根据平行线的性质得出∠C=∠BHF ,从而得出∠BAF=∠BHF ,然后利用AAS判断出△ABF≌△HBF ,根据全等三角形的性质得出AF=FH ; ③ 由 AE=AF,AF=FH得出 AE=FH ,利用两组对边分别平行得四边形是平行四边形得出 四边形FHCG是平行四边形 ,根据平行四边形的性质得出FH=GC ,进而得出AE=GC ,根据等式的性质得出AG=CE ;④根据平行四边形的性质得出FG=HC ,根据三角形全等得出AB=HB ,根据等式的性质得出AB+FG=HB+HC=BC 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】取近似数0.01962≈_______________ (精确到千分位)
-
科目: 来源: 题型:
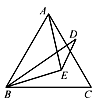
查看答案和解析>>【题目】如图,点E是等边△ABC内一点,且EA=EB,△ABC外一点D满足BD=AC,且BE平分∠DBC,则∠D=.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一张形状是多边形的纸片剪去其中某一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是( )
A. 三角形 B. 四边形 C. 五边形 D. 六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0(其中k为常数).
(1)求证无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知有理数a、b满足(a+2)2+|2b﹣6|=0,则a﹣b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据2、5、6、0、6、1、8的中位数和众数分别是( )
A.0和6
B.0和8
C.5和6
D.5和8
相关试题

