【题目】如图,点E是等边△ABC内一点,且EA=EB,△ABC外一点D满足BD=AC,且BE平分∠DBC,则∠D=.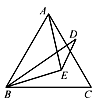
参考答案:
【答案】30°
【解析】(1)连接CE, 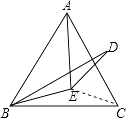
∵△ABC是等边三角形,
∴AC=BC,
在△BCE与△ACE中, 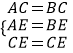
∴△BCE≌△ACE(SSS)
∴∠BCE=∠ACE=30°
∵BE平分∠DBC,
∴∠DBE=∠CBE,
在△BDE与△BCE中, 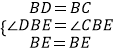
∴△BDE≌△BCE(SAS),
∴∠BDE=∠BCE=30°.
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线,以及对等边三角形的性质的理解,了解等边三角形的三个角都相等并且每个角都是60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )

A.∠1=∠2+∠A
B.∠1=2∠A+∠2
C.∠1=2∠2+2∠A
D.2∠1=∠2+∠A -
科目: 来源: 题型:
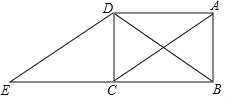
查看答案和解析>>【题目】如图,在矩形ABCD中,连接对角线AC、BD,将△ABC沿BC方向平移,使点B移到点C,得到△DCE.
(1)求证:△ACD≌△EDC;
(2)请探究△BDE的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】取近似数0.01962≈_______________ (精确到千分位)
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一张形状是多边形的纸片剪去其中某一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是( )
A. 三角形 B. 四边形 C. 五边形 D. 六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AC于E,交AD于F,FG∥BC,FH∥AC,下列结论:①AE=AF;②AF=FH;③AG=CE;④AB+FG=BC,其中正确的结论有 . (填序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0(其中k为常数).
(1)求证无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
相关试题

