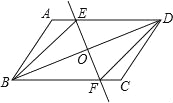
【题目】已知:如图,在ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF;
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.
参考答案:
【答案】(1)证明见解析;
(2)当∠DOE=90°时,四边形BFDE为菱形.
【解析】
试题分析:(1)利用平行四边形的性质以及全等三角形的判定方法得出△DOE≌△BOF(ASA);
(2)首先利用一组对边平行且相等的四边形是平行四边形得出四边形EBFD是平行四边形,进而利用垂直平分线的性质得出BE=ED,即可得出答案.
试题解析:(1)∵在ABCD中,O为对角线BD的中点,
∴BO=DO,∠EDB=∠FBO,
在△EOD和△FOB中
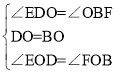 ,
,
∴△DOE≌△BOF(ASA);
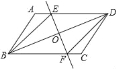
(2)当∠DOE=90°时,四边形BFDE为菱形,
理由:∵△DOE≌△BOF,∴OE=OF,又∵OB=OD,∴四边形EBFD是平行四边形,
∵∠EOD=90°,∴EF⊥BD,∴四边形BFDE为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式x2+ax+b分解因式,得(x+1)(x﹣3),则a,b的值分别是( )
A.a=﹣2,b=﹣3
B.a=2,b=3
C.a=﹣2,b=3
D.a=2,b=﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式计算不正确的是( )
A.(-1)2003=-1
B.-12002=1
C.(-1)2n=1(n为正整数)
D.(-1)2n+1=-1(n为正整数) -
科目: 来源: 题型:
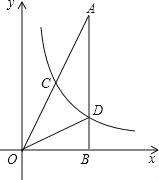
查看答案和解析>>【题目】如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=
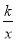 在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.(1)求反比例函数解析式;
(2)求点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中,一元一次方程是( )
A. x2+x=1 B. 3x–5 C. 3+7=10 D. 2x=1
-
科目: 来源: 题型:
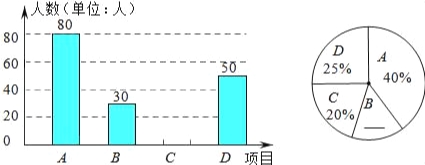
查看答案和解析>>【题目】某中学开展“阳光体育一小时”活动,根据学校实际情况,决定开设A:踢毽子;B:篮球;C:跳绳;D:乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如下两个统计图.
请结合图中的信息解答下列问题:
(1)本次共调查了多少名学生?
(2)请将两个统计图补充完整;
(3)请求出C项目所占的圆心角是 72 度;
(4)若该中学有1200名学生,喜欢篮球运动项目的学生约有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】据报道,目前我国“天河二号”超级计算机的运算速度位居全球第一,其运算速度达到了每秒338 600 000亿次,数字338 600 000用科学记数法可简洁表示为 .
相关试题

