【题目】问题的提出:
如果点![]() 是锐角
是锐角![]() 内一动点,如何确定一个位置,使点
内一动点,如何确定一个位置,使点![]() 到△ABC的三顶点的距离之和
到△ABC的三顶点的距离之和![]() 的值为最小?
的值为最小?
(1)问题的转化:
把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,这样就把确定
,这样就把确定![]() 的最小值的问题转化成确定
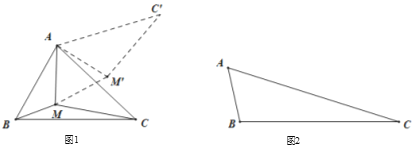
的最小值的问题转化成确定![]() 的最小值的问题了,请你利用图1证明:
的最小值的问题了,请你利用图1证明:![]() .
.
(2)问题的解决:
当点![]() 到锐角
到锐角![]() 的三顶点的距离之和
的三顶点的距离之和![]() 的值为最小时,求
的值为最小时,求![]() 的度数.
的度数.
问题的延伸:
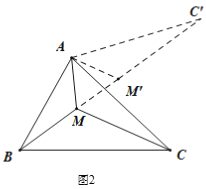
(3)如图2所示,在钝角![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是这个三角形内一动点,请你利用以上方法,求点
是这个三角形内一动点,请你利用以上方法,求点![]() 到这个三角形各顶点的距离之和的最小值.
到这个三角形各顶点的距离之和的最小值.
参考答案:
【答案】(1)证明见解析;(2)∠AMB=120°;(3)![]() .
.
【解析】
(1)证明△AMM'是等边三角形,求出MM'=MA,结合MC=M'C'可得结论;
(2)当B、M、M'、C'在同一直线上时,MA+MB+MC的值为最小,此时∠AMM'=60°,故可得∠AMB=120°;
(3)根据题意作出辅助线,利用旋转的性质求出![]() ,求得
,求得![]() 和
和![]() 的长,然后在
的长,然后在![]() 中,利用勾股定理求出
中,利用勾股定理求出![]() 的长即可.
的长即可.
(1)如图1,由旋转的性质得:∠MAM'=60°,MA=M'A,
∴△AMM'是等边三角形,
∴MM'=MA,
∵MC=M'C',
∴MA+MB+MC=BM+MM′+M′C′;
(2)如图2,把△AMC绕点A逆时针旋转60度得到△AM′C′,连接MM′,由“问题的转化”可知:当B、M、M'、C'在同一直线上时,MA+MB+MC的值为最小,
由(1)可知△AMM'是等边三角形,则∠AMM'=60°,
∴∠AMB=120°;
(3)如图3,把△AMC绕点A旋转60度得到△AM′C′,且B、M、M'、C'在同一直线上,过点![]() 作
作![]() 延长线的垂线
延长线的垂线![]() ,垂足为
,垂足为![]() ,
,
由旋转可得![]() ≌
≌![]() ,则
,则![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
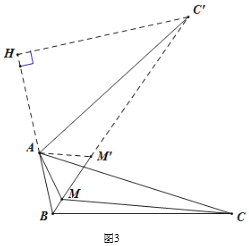
∴![]() ,则
,则![]() ,
,
∴在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵点B、M、M'、C'在同一直线上,
∴在![]() 中,
中,![]() ,
,
即点![]() 到这个三角形各顶点的距离之和的最小值为
到这个三角形各顶点的距离之和的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小丽想用一块面积为
 的正方形纸片,沿着边的方向裁出一块面积为
的正方形纸片,沿着边的方向裁出一块面积为 的长方形纸片,使它的长宽之比为4:3,他不知道能否裁的出来,正在发愁,请你用所学知识帮小丽分析,能否裁出符合要求的纸片.
的长方形纸片,使它的长宽之比为4:3,他不知道能否裁的出来,正在发愁,请你用所学知识帮小丽分析,能否裁出符合要求的纸片. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划购买若干台打印机,现从两家商场了解到同一种型号的打印机报价均为1000元,并且多买都有一定的优惠.各商场的优惠条件如下表所示:
商场
优惠条件
甲商场
第一台按原价收费,其余的每台优惠15%
乙商场
每台优惠10%
(1)设公司购买
 台打印机,选择甲商场时,所需费用为
台打印机,选择甲商场时,所需费用为 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为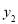 元,请分别求出
元,请分别求出 ,
,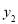 与
与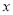 之间的关系式.
之间的关系式.(2)什么情况下,两家商场的收费相同?什么情况下,到甲商场购买更优惠?什么情况下,到乙商场购买更优惠?
(3)现从甲乙两商场一共买入10台打印机,已知甲商场的运费为每台15元,乙商场的运费为每台20元,设总运费为
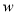 元,从甲商场购买
元,从甲商场购买 台打印机,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
台打印机,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点
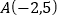 ,
, ,
, ,点
,点 是三角形
是三角形 边
边 上任意一点,三角形经过平移后得到三角形
上任意一点,三角形经过平移后得到三角形 ,点
,点 的对应点为
的对应点为 .
.
(1)直接写出点
 的坐标______________.
的坐标______________.(2)画出三角形
 平移后的三角形
平移后的三角形 .
.(3)在
 轴上是否存在一点
轴上是否存在一点 ,使三角形
,使三角形 的面积等于三角形
的面积等于三角形 面积的
面积的 ,若存在,请求出点
,若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
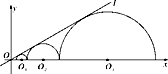
查看答案和解析>>【题目】如图,圆心都在x轴正半轴上的半圆O1 , 半圆O2 , …,半圆On与直线l相切.设半圆O1 , 半圆O2 , …,半圆On的半径分别是r1 , r2 , …,rn , 则当直线l与x轴所成锐角为30°,且r1=1时,r2018=.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋中装有3个带号码的球,球号分别为2,3,4,这些球除号码不同外其它均相同。甲、乙、两同学玩摸球游戏,游戏规则如下:
先由甲同学从中随机摸出一球,记下球号,并放回搅匀,再由乙同学从中随机摸出一球,记下球号。将甲同学摸出的球号作为一个两位数的十位上的数,乙同学的作为个位上的数。若该两位数能被4整除,则甲胜,否则乙胜.
问:这个游戏公平吗?请说明理由。
相关试题

