【题目】如图,在平行四边形ABCD中,AE、BF分别平分∠DAB和∠ABC,交CD于点E、F,AE、BF相交于点M.
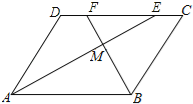
(1)试说明:AE⊥BF;
(2)判断线段DF与CE的大小关系,并予以说明.
参考答案:
【答案】(1)证明见解析;(2)DF=CE,理由见解析.
【解析】试题分析:(1)利用平行四边形的性质得到AD∥BC,然后得到∠DAB+∠ABC=180°,然后根据角的平分线得出∠DAB=2∠BAE,∠ABC=2∠ABF,等量代换得出∠BAE+∠ABF=90°即可;(2)先猜想DF=CE,利用角的平分线和平行线的性质可得DE=AD,CF=BC,然后利用线段的和差关系可得出结论.
试题解析:(1)∵在平行四边形ABCD中,AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE、BF分别平分∠DAB和∠ABC,
∴∠DAB=2∠BAE,∠ABC=2∠ABF.
∴2∠BAE+2∠ABF=180°.
即∠BAE+∠ABF=90°.
∴∠AMB=90°.
∴AE⊥BF.
(2)DF=CE,
∵在平行四边形ABCD中,CD∥AB,
∴∠DEA=∠EAB.
又∵AE平分∠DAB,
∴∠DAE=∠EAB.∴∠DEA=∠DAE.
∴DE=AD.
同理可得,CF=BC.
又∵在平行四边形ABCD中,AD=BC,
∴DE=CF.
∴DE﹣EF=CF﹣EF.
即DF=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列数据不能用有序数对表示的是( )
A. 4楼,5楼 B. 6楼,8号 C. 3号路,25号 D. 东经110°,北纬67°
-
科目: 来源: 题型:
查看答案和解析>>【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:
“读书节”活动计划书
书本类别
A类
B类
进价(单位:元)
18
12
备注
1、用不超过16800元购进A、B两类图书共1000本;
2、A类图书不少于600本;
…
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买的图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A、B两类图书的标价;
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=x+b的图象与反比例函数y=
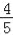 (k为常数,k≠0)的图象交于点A(﹣1,4)和点B(a,1).
(k为常数,k≠0)的图象交于点A(﹣1,4)和点B(a,1).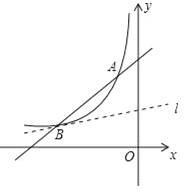
(1)求反比例函数的表达式和a、b的值;
(2)若A、O两点关于直线l对称,请连接AO,并求出直线l与线段AO的交点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知m是方程x2-x-2=0的一个根,则代数式m2-m+2的值等于( )
A. 4 B. 1 C. 0 D. -1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的各个外角都是40°,那么这个多边形的内角和是____度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正八边形的每个外角为______度.
相关试题

