Question

【题目】如图，抛物线y=﹣x2﹣2x+3 的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C

（1）求A、B、C的坐标；
（2）过抛物线上一点F作y轴的平行线，与直线AC交于点G．若FG= AC，求点F的坐标；
（3）E（0，﹣2），连接BE．将△OBE绕平面内的某点逆时针旋转90°得到△O′B′E′，O、B、E的对应点分别为O′、B′、E′．若点B′、E′两点恰好落在抛物线上，求点B′的坐标．

Answer 1

【答案】
（1）

解：对于抛物线y=﹣x2﹣2x+3，

令x=0得y=3，∴C（0，3），

令y=0，则﹣x2﹣2x+3=0解得x=﹣3或1，

∴A（﹣3，0）；B（1，0）；C（0，3）

（2）

解：如图1中，

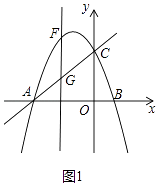
∵A（﹣3，0），C（03），

∴直线AC解析式为y=x+3，OA=OC=3，

∴AC=3 ，FG= AC=2

设F（m，﹣m2﹣2m+3），则G（m，m+3），

则|﹣m2﹣2m+3﹣（m+3）|=2，

解得m=﹣1或﹣2或 或 ，

则F点的坐标为（﹣1，4）或（﹣2，3）或（ ， ）或（ ， ）

（3）

解：如图2中，旋转90°后，对应线段互相垂直且相等，则BE与B’E’互相垂直且相等．

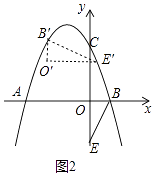
设B’（t，﹣t2﹣2t+3），则E’（t+2，﹣t2﹣2t+3﹣1）

∵E’在抛物线上，则﹣（t+2）2﹣2（t+2）+3=﹣t2﹣2t+3﹣1，

解得，t=﹣ ，则B’的坐标为（﹣ ， ）

【解析】（1）对于抛物线分别令x=0，y=0即可解决问题．（2）先求出AC的解析式，由题意可知FG=2，设F（m，﹣m2﹣2m+3），则G（m，m+3），则有|﹣m2﹣2m+3﹣（m+3）|=2，解方程即可．（3）如图2中，旋转90°后，对应线段互相垂直且相等，则BE与B’E’互相垂直且相等．设B’（t，﹣t2﹣2t+3），则E’（t+2，﹣t2﹣2t+3﹣1）．因为E’在抛物线上，则有﹣（t+2）2﹣2（t+2）+3=﹣t2﹣2t+3﹣1，解方程即可．
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．