【题目】如图,D是等边三角形ABC中BA延长线上一点,连接CD,E是BC上一点,且DE=DC,若BD+BE=![]() ,CE=
,CE=![]() ,则这个等边三角形的边长是__________.
,则这个等边三角形的边长是__________.
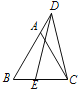
参考答案:
【答案】![]()
【解析】
作EK∥AC交AB于K,根据平行线的性质可得出△BEK是等边三角形,∠DKE=∠DAC,故EK=BE,再根据DE=DC可知∠DEC=∠DCE,由三角形外角的性质可知∠B+∠KDE=∠DEC,因为∠DCA+∠ACB=∠DCE,故可得出∠B+∠KDE=∠DCA+∠ACB,再由∠B=∠ACB=60°可知∠KDE=∠DCA,故可得出△EKD≌△DAC,故AD=DK,进而可得BE=AD.根据BD+BC+CE=3AB即可得出结论.
作EK∥AC交AB于K.
∵△ABC是等边三角形,∴∠B=∠ACB=∠BAC=60°,AB=BC=AC.
∵EK∥AC,∠BKE=∠BAC=60°,∠KEB=∠ACB=60°,∴△BEK是等边三角形,∠DKE=∠DAC,∴EK=BE=BK.
∵DE=DC,∴∠DEC=∠DCE,∴∠B+∠KDE=∠DCA+∠ACB.
∵∠B=∠ACB=60°,∴∠KDE=∠DCA.
在△EKD与△DAC中,∵∠DKE=∠DAC,∠KDE=∠DCA,DE=DC,∴△EKD≌△DAC(AAS),∴AD=EK,∴BE=AD.
∵BD+BE=![]() ,CE=
,CE=![]() ,∴BD+BE+2CE=
,∴BD+BE+2CE=![]() ,∴BA+AD+BC+EC=3BA=
,∴BA+AD+BC+EC=3BA=![]() ,∴AB=
,∴AB=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上两点A、B,其中A表示的数为-2,B表示的数为2,若在数轴上存在一点C,使得AC+BC=n,则称点C叫做点A、B的“n节点”.例如图1所示:若点C表示的数为0,有AC+BC=2+2=4,则称点C为点A、B的“4节点”.
请根据上述规定回答下列问题:
(1)若点C为点A、B的“n节点”,且点C在数轴上表示的数为-4,求n的值;
(2)若点D是数轴上点A、B的“5节点”,请你直接写出点D表示的数为______;
(3)若点E在数轴上(不与A、B重合),满足BE=
 AE,且此时点E为点A、B的“n节点”,求n的值.
AE,且此时点E为点A、B的“n节点”,求n的值.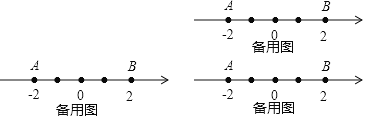
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E.F分别在AB、CD上,AE=CF,连接AF,BF,DE,CE,分别交于H、G.
求证:(1)四边形AECF是平行四边形。(2)EF与GH互相平分。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把△ABC沿EF对折,叠合后的图形如图所示.若∠A=60°,∠1=90°,则∠2的度数为( )
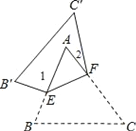
A. 24°B. 25°C. 30°D. 35°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt
 中,∠
中,∠
 90°,
90°, ,
, 平分
平分 .
.(1)尺规作图:作线段
 的垂直平分线
的垂直平分线 ;(要求:保留作图痕迹,不写作法)
;(要求:保留作图痕迹,不写作法)
(2)记直线
 与
与 ,
, 的交点分别是点
的交点分别是点 ,
, .当
.当 时,求
时,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一只不透明的袋子中装有2个白球和1个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球(不放回),再从余下的2个球中任意摸出1个球.
(1)用树状图或列表等方法列出所有可能出现的结果;
(2)求两次摸到的球的颜色不同的概率. -
科目: 来源: 题型:
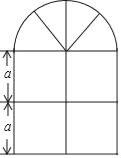
查看答案和解析>>【题目】如图,某种窗户由上下两部分组成,其上部是用木条围成的半圆形,且半圆内部用了三根等长的木条分隔,下部是用木条围成的边长相同的四个小正方形,木条宽厚不计,已知下部的小正方形的边长为a米.
(1)用含a的式子分别表示窗户的面积和木条用料(实线部分)的总长;
(2)若a=1,窗户上安装的是玻璃,玻璃每平方米25元,木条每米20元,求制作这扇窗户需要多少元?(π取3,结果精确到个位)
相关试题

