【题目】如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=3. 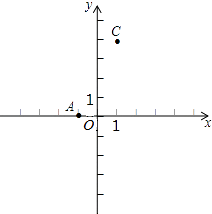
(1)求点B的坐标;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:点B在点A的右边时,﹣1+3=2,
点B在点A的左边时,﹣1﹣3=﹣4,
所以,B的坐标为(2,0)或(﹣4,0)
(2)解:△ABC的面积= ![]() ×3×4=6
×3×4=6
(3)解:设点P到x轴的距离为h,
则 ![]() ×3h=10,
×3h=10,
解得h= ![]() ,
,
点P在y轴正半轴时,P(0, ![]() ),
),
点P在y轴负半轴时,P(0,﹣ ![]() ),
),
综上所述,点P的坐标为(0, ![]() )或(0,﹣
)或(0,﹣ ![]() ).
).
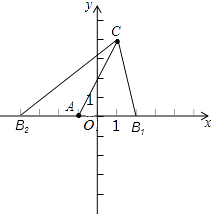
【解析】(1)分点B在点A的左边和右边两种情况解答;(2)利用三角形的面积公式列式计算即可得解;(3)利用三角形的面积公式列式求出点P到x轴的距离,然后分两种情况写出点P的坐标即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题:大家知道
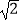 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 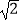 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用 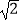 ﹣1来表示
﹣1来表示 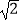 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为 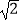 的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<(
的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<( 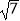 )2<32 , 即2<
)2<32 , 即2< 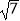 <3,∴
<3,∴ 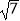 的整数部分为2,小数部分为(
的整数部分为2,小数部分为( 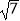 ﹣2). 请解答:
﹣2). 请解答:
(1)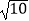 的整数部分是 , 小数部分是
的整数部分是 , 小数部分是
(2)如果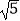 的小数部分为a,
的小数部分为a, 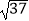 的整数部分为b,求a+b﹣
的整数部分为b,求a+b﹣ 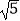 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,CD与CE分别是斜边AB上的高与中线,则下列结论:①BE=BC;②∠DCB=∠A;③∠DCB=∠ACE;④
 ,其中正确的结论是_____.
,其中正确的结论是_____.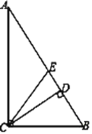
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点A(a,b),将OA绕坐标原点O逆时针旋转90°至OA',则点A'的坐标是_______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1和∠2互为补角,∠A=∠D.求证:AB∥CD.
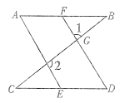
证明:∵∠1与∠CGD是对顶角,
∴∠1=∠CGD(______).
又∠1和∠2互为补角(已知),
∴∠CGD和∠2互为补角,
∴AE∥FD(_________),
∴∠A=∠BFD(_______).
∵∠A=∠D(已知),
∴∠BFD=∠D(_______),
AB∥CD(______).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB∥DF,∠D+∠B=180°,

(1)求证:DE∥BC;
(2)如果∠AMD=75°,求∠AGC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学现有在校学生2150人,为了解该校学生的课余活动情况,采取随机抽样的方法从阅读、运动、娱乐、其它四个方面调查了若干名学生,并将调查的结果绘制了如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
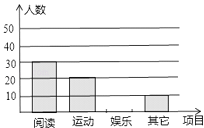
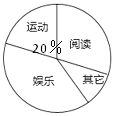
(1)本次调查共抽取了多少名学生?
(2)通过计算补全条形图,并求出扇形统计图中阅读部分圆心角的度数;
(3)请你估计该中学在课余时间参加阅读和其它活动的学生一共有多少名?
相关试题

