【题目】某市为了美化环境,计划在一定的时间内完成绿化面积![]() 万亩的任务,后来市政府调整了原定计划,不但绿化面积要在原计划的基础上增加
万亩的任务,后来市政府调整了原定计划,不但绿化面积要在原计划的基础上增加![]() ,而且要提前
,而且要提前![]() 年完成任务,经测算要完成新的计划,平均每年的绿化面积必须比原计划多
年完成任务,经测算要完成新的计划,平均每年的绿化面积必须比原计划多![]() 万亩,求原计划平均每年的绿化面积.
万亩,求原计划平均每年的绿化面积.
参考答案:
【答案】原计划平均每年完成绿化面积![]() 万亩.
万亩.
【解析】
本题的相等关系是:原计划完成绿化时间实际完成绿化实际=1.设原计划平均每年完成绿化面积x万亩,则原计划完成绿化完成时间![]() 年,实际完成绿化完成时间:
年,实际完成绿化完成时间:![]() 年,列出分式方程求解
年,列出分式方程求解
解:设原计划平均每年完成绿化面积![]() 万亩.
万亩.
根据题意可列方程:
![]()
去分母整理得:![]()
解得:![]() ,
,![]()
经检验:![]() ,
,![]() 都是原分式方程的根,因为绿化面积不能为负,所以取
都是原分式方程的根,因为绿化面积不能为负,所以取![]() .
.
答:原计划平均每年完成绿化面积![]() 万亩.
万亩.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m).
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数
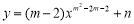 的图像
的图像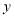 随
随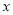 增大而减小,且经过点
增大而减小,且经过点 .
.求(1)
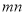 的值;
的值;(2)求该直线与坐标轴围成的三角形的面积及坐标原点到直线的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的
 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)甲
乙
进价(元/件)
22
30
售价(元/件)
29
40
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】厉害了,我的国!2018年10月24日,珠港澳大桥建成通车,成了世界瞩目的焦点.这座连接中国珠海、香港、澳门三座城市,全长55公里,投资1269亿元经过6年筹备与9年建设的跨海大桥,创造了400多项专利和七项世界之最,被誉为世界的第七大奇迹,是中国科技实力的伟大展现,令全球华人倍感骄傲与自豪.用科学记数法表示大桥的投资款正确的是( )
A.12.69×
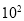 亿元B.1.269×
亿元B.1.269×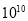 元
元C.1.269×
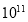 元D.1.269×
元D.1.269×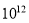 元
元 -
科目: 来源: 题型:
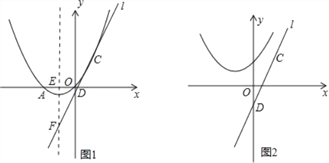
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c经过原点O及点A(﹣4,0)和点C(2,3).
(1)求抛物线的解析式及顶点坐标;
(2)如图1,设抛物线的对称轴与x轴交于点E,将直线y=2x沿y轴向下平移n个单位后得到直线l,若直线l经过C点,与y轴交于点D,且与抛物线的对称轴交于点F.若P是抛物线上一点,且PC=PF,求点P的坐标;
(3)如图2,将(1)中所求抛物线向上平移4个单位得到新抛物线,求新抛物线上到直线CD距离最短的点的坐标.(直接写出结果,不要解答过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标平面内,
 为原点,点
为原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
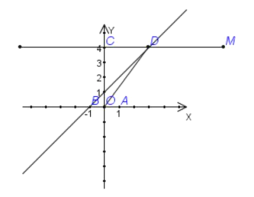
的坐标为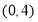 ,直线
,直线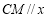 轴. 点
轴. 点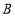 与点
与点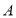 关于原点对称,直线
关于原点对称,直线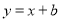 (
(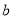 为常数)经过点
为常数)经过点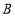 ,且与直线
,且与直线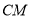 相交于点
相交于点 .
.
(1)求
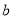 的值和点
的值和点 的坐标;
的坐标;(2)在
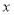 轴上有一点
轴上有一点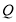 ,使
,使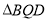 的面积为
的面积为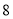 ,求
,求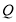 点的坐标;
点的坐标; (3)在
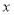 轴的正半轴上是否存在一点
轴的正半轴上是否存在一点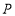 ,使得
,使得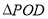 为等腰三角形,若存在,求出点
为等腰三角形,若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
相关试题

