【题目】如图,点C是线段AB上一点,D是线段CB的中点,已知图中所有的线段的长度之和为23,线段AC的长度与线段CB的长度都是正整数,则线段AC长 . ![]()
参考答案:
【答案】3
【解析】解:设AC=y,CD=BD=x,则AC+CD+DB+AD+AB+CB=23,
即:y+x+x+(x+y)+(2x+y)+2x=23,
得:7x+3y=23,
因为线段AC的长度与线段CB的长度都是正整数,
所以可知x最大为3,
可知:x=3,y为小数,不符合;
x=2,y=3,符合题意;
x=1,y为小数,不符合.
所以AC=3,
所以答案是:3.
【考点精析】认真审题,首先需要了解两点间的距离(同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市对初二综合素质测评中的审美与艺术进行考核,规定如下:考核综合评价得分由测试成绩(满分100分)和平时成绩(满分100分)两部分组成,其中测试成绩占80%,平时成绩占20%,并且当综合评价得分大于或等于80分时,该生综合评价为A等.
(1)孔明同学的测试成绩和平时成绩两项得分之和为185分,而综合评价得分为91分,则孔明同学测试成绩和平时成绩各得多少分?
(2)某同学测试成绩为70分,他的综合评价得分有可能达到A等吗?为什么?
(3)如果一个同学综合评价要达到A等,他的测试成绩至少要多少分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果|a+2|和(b﹣1)2互为相反数,那么(a+b)2015的值是( )
A. -2015 B. 2015 C. -1 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=c,AC=b.AD是△ABC的角平分线,DE⊥A于E,DF⊥AC于F,EF与AD相交于O,已知△ADC的面积为1.
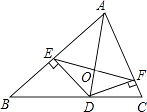
(1)证明:DE=DF;
(2)试探究线段EF和AD是否垂直?并说明理由;
(3)若△BDE的面积是△CDF的面积2倍.试求四边形AEDF的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了“绿色出行”,减少雾霾,家住番禺在广州中心城区上班的王经理,上班出行由自驾车改为乘坐地铁出行,已知王经理家距上班地点21千米,他用地铁方式平均每小时出行的路程,比他用自驾车平均每小时行驶的路程的2倍还多5千米,他从家出发到达上班地点,地铁出行所用时间是自驾车方式所用时间的
 .求王经理地铁出行方式上班的平均速度.
.求王经理地铁出行方式上班的平均速度. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中有三个点A(1,﹣1)、B(﹣1,﹣1)、C(0,1),点P(0,2)关于A的对称点为P1,P1关于B的对称点P2,P2关于C的对称点为P3,按此规律继续以A、B、C为对称中心重复前面的操作,依次得到P4,P5,P6,…,则点P2015的坐标是( )
A.(0,0) B.(0,2) C.(2,﹣4) D.(﹣4,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|﹣2|+(﹣1)2012﹣(π﹣4)0 .
相关试题

