【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,交y轴于点C,且B(1,0),C(0,3),将△BOC绕点O按逆时针方向旋转90°,C点恰好与A重合.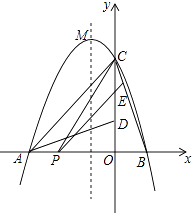
(1)求该二次函数的解析式;
(2)若点P为线段AB上的任一动点,过点P作PE∥AC,交BC于点E,连结CP,求△PCE面积S的最大值;
(3)设抛物线的顶点为M,Q为它的图象上的任一动点,若△OMQ为以OM为底的等腰三角形,求Q点的坐标.
参考答案:
【答案】
(1)
解:∵B(1,0),C(0,3),
∴OB=1,OC=3.
∵△BOC绕点O按逆时针方向旋转90°,C点恰好与A重合.
∴OA=OC=3,
∴A(﹣3,0),
∵点A,B,C在抛物线上,
∴ 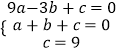 ,
,
∴ 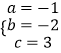 ,
,
∴二次函数的解析式为y=﹣x2﹣2x+3
(2)
解:设点P(x,0),则PB=1﹣x,
∵A(﹣3,0),B(1,0),
∴AB=4,
∵C(0,3),
∴OC=3,
∴S△ABC= ![]() AB×OC=6,
AB×OC=6,
∵PE∥AC,
∴△BPE∽△BAC,
∴ ![]() ,
,
∴S△PBE= ![]() (1﹣x)2,
(1﹣x)2,
∴S△PCE=S△PBC﹣S△PBE= ![]() PB×OC﹣
PB×OC﹣ ![]() (1﹣x)2=
(1﹣x)2= ![]() (1﹣x)×3﹣
(1﹣x)×3﹣ ![]() (1﹣x)2=﹣
(1﹣x)2=﹣ ![]() (x+1)2+
(x+1)2+ ![]() ,
,
当x=﹣1时,S△PCE的最大值为 ![]()
(3)
解:∵二次函数的解析式为y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴顶点坐标(﹣1,4),
∵△OMQ为等腰三角形,OM为底,
∴MQ=OQ,
∴ ![]() =
= ![]() ,
,
∴8x2+18x=7=0,
∴x= ![]() ,
,
∴y= ![]() 或y=
或y= ![]() ,
,
∴Q( ![]() ,
, ![]() ),或(
),或( ![]() ,
, ![]() )
)
【解析】(1)先求出点A坐标,再用待定系数法求出抛物线解析式;(2)先求出S△PCE=S△PBC﹣S△PBE=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,即可求出最大面积;(3)先求出抛物线顶点坐标,由等腰三角形的两腰相等建立方程求出点Q坐标.
,即可求出最大面积;(3)先求出抛物线顶点坐标,由等腰三角形的两腰相等建立方程求出点Q坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形MNPQ网格中,每个小方格的边长都相等,正方形ABCD的顶点在正方形MNPQ的小方格顶点上.

(1)设正方形MNPQ网格内的每个小方格的边长为1,求:
①△ABQ,△BCM,△CDN,△ADP的面积;
②正方形ABCD的面积;
(2)设MB=a,BQ=b,利用这个图形中的直角三角形和正方形的面积关系,你能验证勾股定理吗?相信你能给出简明的推理过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角△ABC中,AC=10,S△ABC =25,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值是( )

A. 4 B.
 C. 5 D. 6
C. 5 D. 6 -
科目: 来源: 题型:
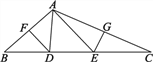
查看答案和解析>>【题目】如图,△ABC中,∠BAC=110°,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,BC=10cm.求:
(1)△ADE的周长;
(2)∠DAE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一水果贩子在批发市场按每千克1.8元批发了若干千克的西瓜进城出售,为方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出西瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:

(1)农民自带的零钱是多少?
(2)降价前每千克西瓜出售的价格是多少?
(3)随后他按每千克下降0.5元将剩余的西瓜售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了多少千克的西瓜?
(4)请问这个水果贩子一共赚了多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为( )

A.2
B.3
C.4
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于
 AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
A. 2 B.
 C.
C.  D.
D. 
相关试题

