【题目】如图,正方形MNPQ网格中,每个小方格的边长都相等,正方形ABCD的顶点在正方形MNPQ的小方格顶点上.

(1)设正方形MNPQ网格内的每个小方格的边长为1,求:
①△ABQ,△BCM,△CDN,△ADP的面积;
②正方形ABCD的面积;
(2)设MB=a,BQ=b,利用这个图形中的直角三角形和正方形的面积关系,你能验证勾股定理吗?相信你能给出简明的推理过程.
参考答案:
【答案】(1)①6;②25;(2)见解析
【解析】试题分析:(1)根据直角三角形的面积公式:S=两条直角边的乘积的一半进行计算;
(2)根据面积能够验证勾股定理.
试题解析:解:(1)∵网格中每个小正方形的边长为1,由图可知AQ=3,BQ=4,∠Q=90°,∴S△ABQ=![]() AQBQ=6;同理S△BCM=S△CDN=S△ADP=6.
AQBQ=6;同理S△BCM=S△CDN=S△ADP=6.
又∵MQ=7,∴S正方形MNPQ=49,∴S正方形ABCD=S正方形MNPQ﹣4S△ABQ=49﹣4×6=25.
(2)能够验证勾股定理.理由如下:
在△BCM、△ABQ中,∵∠M=∠Q=∠ABC=90°,∴∠MBC=∠QAB.
又∵AB=BC,∴△BCM≌△ABQ.
同理△CDN≌△DAP≌△BCM.
∵MB=a,BQ=b,S正方形ABCD=S正方形MNPQ﹣4S△ABQ,∴AB2=(a+b)2﹣4×![]() ab,即AB2=a2+b2.
ab,即AB2=a2+b2.
设AB=c,得c2=a2+b2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”。如图,在三角形ABC中,∠C=90°,较短的一条直角边BC=1,且三角形ABC是“有趣三角形”,求三角形ABC的“有趣中线”的长。
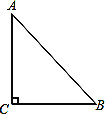
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量得这个零件各边尺寸如图2所示.

图1 图2
(1)你认为这个零件符合要求吗?为什么?
(2)求这个零件的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某地由于居民增多,要在公路边增加一个公共汽车站,A,B是路边两个新建小区,这个公共汽车站建在什么位置,能使两个小区到车站的路程一样长?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角△ABC中,AC=10,S△ABC =25,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值是( )

A. 4 B.
 C. 5 D. 6
C. 5 D. 6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=110°,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,BC=10cm.求:
(1)△ADE的周长;
(2)∠DAE的度数.
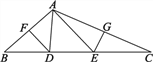
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,交y轴于点C,且B(1,0),C(0,3),将△BOC绕点O按逆时针方向旋转90°,C点恰好与A重合.
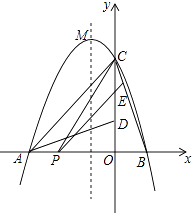
(1)求该二次函数的解析式;
(2)若点P为线段AB上的任一动点,过点P作PE∥AC,交BC于点E,连结CP,求△PCE面积S的最大值;
(3)设抛物线的顶点为M,Q为它的图象上的任一动点,若△OMQ为以OM为底的等腰三角形,求Q点的坐标.
相关试题

