【题目】如图,在直角坐标平面内有两点A(0,2)、B(﹣2,0)、C(2,0).
(1)△ABC的形状是 等腰直角三角形;
(2)求△ABC的面积及AB的长;
(3)在y轴上找一点P,如果△PAB是等腰三角形,请直接写出点P的坐标.

参考答案:
【答案】(1)等腰直角三角形,(2)![]() ;(3)P(0,2)或P(0,﹣2)或P(0,2﹣
;(3)P(0,2)或P(0,﹣2)或P(0,2﹣![]() )或P(0,2+
)或P(0,2+![]() )或P(0,0).
)或P(0,0).
【解析】试题分析:(1)根据点的坐标判断出OA=OB=OC,从而得出结论;
(2)根据点的坐标求出求出BC,OA,再用三角形面积公式即可;
(3)设出点P坐标,根据平面坐标系中,两点间的距离公式表示出BP,AP,再分三种情况计算即可.
试题解析:∵A(0,2)、B(﹣2,0)、C(2,0).
∴OB=OC=OA,
∴△ABC是等腰三角形,
∵AO⊥BC,
∴△ABC是等腰直角三角形.
故答案为等腰直角三角形,
(2)∵A(0,2)、B(﹣2,0)、C(2,0).
∴BC=4,OA=2,
∴S△ABC=![]() BC×AO=
BC×AO=![]() ×4×2=4,
×4×2=4,
∵A(0,2)、B(﹣2,0),
∴AB=![]() ,
,
(3)设点P(0,m),
∵A(0,2)、B(﹣2,0),
∴AB=2![]() ,BP=
,BP=![]() ,AP=|m﹣2|,
,AP=|m﹣2|,
∵△PAB是等腰三角形,
∴①当AB=BP时,
∴2![]() =
=![]() ,
,
∴m=±2,
∴P(0,2)或P(0,﹣2),
②当AB=AP时,
∴2![]() =|m﹣2|,
=|m﹣2|,
∴m=2+2![]() 或m=2﹣2
或m=2﹣2![]() ,
,
∴P(0,2﹣2![]() )或P(0,2+2
)或P(0,2+2![]() )
)
③当AP=BP时,
∴|m﹣2|=![]() ,
,
∴m=0,
∴P(0,0),
∴P(0,2)或P(0,﹣2)或P(0,2﹣2![]() )或P(0,2+2
)或P(0,2+2![]() )或P(0,0).
)或P(0,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】图中是抛物线型拱桥,P处有一照明灯,水面OA宽4m,从O,A两处观测P处,仰角分别为α,β,tanα=
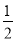 ,tanβ=
,tanβ= ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系.(1)求点P的坐标;
(2)水面上升1m,水面宽多少(
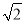 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?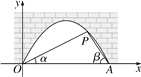
-
科目: 来源: 题型:
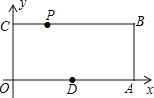
查看答案和解析>>【题目】已知,如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,动点P在线段BC上以每秒2个单位长的速度由点C向B 运动.设 动点P的运动时间为t秒
(1)当t为何值时,四边形PODB是平行四边形?
(2)在直线CB上是否存在一点Q,使得O、D、Q、P四点为顶点的四边形是菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由。
(3) 在线段PB上有一点M,且PM=5,当P运动 秒时,四边形OAMP的周长最小, 并画图标出点M的位置。

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,求旗杆的高度OM和玛丽在荡绳索过程中离地面的最低点的高度MN.

-
科目: 来源: 题型:
查看答案和解析>>【题目】请根据证明过程,在括号内填写相应理由,如图,已知B、E分别是AC、DF上的点,∠1=∠2,∠C=∠D,
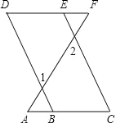
求证:∠A=∠F.
证明:因为∠1=∠2(已知)
所以BD∥CE( )所以∠C=∠ABD( )因为∠C=∠D( )
所以∠D=∠ABD( )
所以DF∥AC( )所以∠A=∠F( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】汽车在行驶的过程中速度往往是变化的,如图表示一辆汽车的速度随时间变化而变化的情况.
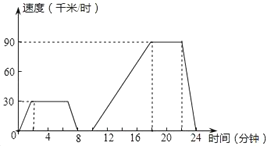
(1)汽车从出发到最后停止共经过了多少时间?它的最高时速是多少?
(2)汽车在哪些时间段保持匀速行驶?时速分别是多少?
(3)汽车出发8min到10min之间可能发生了什么情况?
(4)求汽车从出发后第18分钟到第22分钟行驶的路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿CE折叠后,使点D恰好落在对角线AC上的点F处.
(1)求EF的长;
(2)求梯形ABCE的面积.

相关试题

