【题目】汽车在行驶的过程中速度往往是变化的,如图表示一辆汽车的速度随时间变化而变化的情况.
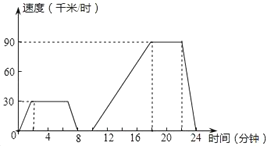
(1)汽车从出发到最后停止共经过了多少时间?它的最高时速是多少?
(2)汽车在哪些时间段保持匀速行驶?时速分别是多少?
(3)汽车出发8min到10min之间可能发生了什么情况?
(4)求汽车从出发后第18分钟到第22分钟行驶的路程.
参考答案:
【答案】(1)汽车从出发到最后停止共经过了24min,它的最高时速是90km/h;(2)汽车在2min到6min,18min到22min保持匀速行驶,时速分别是30km/h和90km/h;(3)汽车出发8min到10min之间处于静止状态,可能是遇到红灯等情况;(4)6km.
【解析】
利用函数图象中横、纵坐标的意义分别求解即可.
解:(1)汽车从出发到最后停止共经过了24min,它的最高时速是90km/h;
(2)汽车在2min到6min,18min到22min保持匀速行驶,时速分别是30km/h和90km/h;
(3)汽车出发8min到10min之间处于静止状态,可能是遇到红灯等情况;
(4)汽车从出发后第18分钟到第22分钟行驶的路程=![]() (km)
(km)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,求旗杆的高度OM和玛丽在荡绳索过程中离地面的最低点的高度MN.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标平面内有两点A(0,2)、B(﹣2,0)、C(2,0).
(1)△ABC的形状是 等腰直角三角形;
(2)求△ABC的面积及AB的长;
(3)在y轴上找一点P,如果△PAB是等腰三角形,请直接写出点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】请根据证明过程,在括号内填写相应理由,如图,已知B、E分别是AC、DF上的点,∠1=∠2,∠C=∠D,
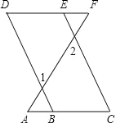
求证:∠A=∠F.
证明:因为∠1=∠2(已知)
所以BD∥CE( )所以∠C=∠ABD( )因为∠C=∠D( )
所以∠D=∠ABD( )
所以DF∥AC( )所以∠A=∠F( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿CE折叠后,使点D恰好落在对角线AC上的点F处.
(1)求EF的长;
(2)求梯形ABCE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=-
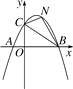
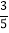 [(x-2)2+n]与x轴交于点A(m-2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连接BC.
[(x-2)2+n]与x轴交于点A(m-2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连接BC.(1)求m,n的值;
(2)点N为抛物线上的一动点,且位于直线BC上方,连接CN,BN.求△NBC面积的最大值.
-
科目: 来源: 题型:
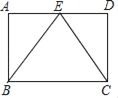
查看答案和解析>>【题目】如图,在矩形ABCD中,点E是边AD的中点,连接BE、CE.
(1)求证:△ABE≌△DCE;
(2)当BC=2AB,求∠BEC的大小.
相关试题

