【题目】如图,已知抛物线![]() 图象经过A(﹣1,0),B(4,0)两点.
图象经过A(﹣1,0),B(4,0)两点.

(1)求抛物线的解析式;
(2)若C(m,m﹣1)是抛物线上位于第一象限内的点,D是线段AB上的一个动点(不与端点A、B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
①求证:四边形DECF是矩形;
②试探究:在点D运动过程中,DE、DF、CF的长度之和是否发生变化?若不变,求出它的值;若变化,试说明变化情况.
参考答案:
【答案】(1) ![]() ;(2)①证明见解析; ②不变,
;(2)①证明见解析; ②不变, ![]() .
.
【解析】试题分析:(1)根据待定系数法即可求得;
(2)把C(m,m-1)代入y=-![]() x2+
x2+![]() x+2求得点C的坐标,从而求得AH=4,CH=2,BH=1,AB=5,然后根据
x+2求得点C的坐标,从而求得AH=4,CH=2,BH=1,AB=5,然后根据![]() =2,∠AHC=∠BHC=90°得出△AHC∽△CHB,根据相似三角形的对应角相等求得∠ACH=∠CBH,因为∠CBH+∠BCH=90°所以∠ACH+∠BCH=90°从而求得∠ACB=90°,先根据有两组对边平行的四边形是平行四边形求得四边形DECF是平行四边形,进而求得□DECF是矩形;
=2,∠AHC=∠BHC=90°得出△AHC∽△CHB,根据相似三角形的对应角相等求得∠ACH=∠CBH,因为∠CBH+∠BCH=90°所以∠ACH+∠BCH=90°从而求得∠ACB=90°,先根据有两组对边平行的四边形是平行四边形求得四边形DECF是平行四边形,进而求得□DECF是矩形;
(3)根据矩形的对角线相等,求得EF=CD,因为当CD⊥AB时,CD的值最小,此时CD的值为2,所以EF的最小值是2;
试题解析:
(1)∵抛物线y=﹣![]() +bx+c图象经过A(﹣1,0),B(4,0)两点,
+bx+c图象经过A(﹣1,0),B(4,0)两点,
根据题意,得
解得
∴抛物线的解析式为: ![]() ;
;
(2)①证明:把C(m,m﹣1)代入![]() 得
得
![]() ,
,
解得:m=3或m=﹣2,
∵C(m,m﹣1)位于第一象限,
∴![]()
∴m>1,
∴m=﹣2不合舍去,只取m=3,
∴点C坐标为(3,2).
如图,过C点作CH⊥AB,垂足为H,则∠AHC=∠BHC=90°,

由A(﹣1,0)、B(3,0)、C(3,2)得 AH=4,CH=2,BH=1,AB=5
∵![]() ∠AHC=∠BHC=90°
∠AHC=∠BHC=90°
∴△AHC∽△CHB,
∴∠ACH=∠CBH,
∵∠CBH+∠BCH=90°
∴∠ACH+∠BCH=90°
∴∠ACB=90°,
∵DE∥BC,DF∥AC,
即四边形DECF是平行四边形,
∴四边形DECF是矩形;
(3)∵DE∥BC
∴ΔAED∽ΔACB
∴![]() (1)
(1)
同理: ![]() (2)
(2)
设![]() , 则
, 则![]()
由(1)得![]()
∴![]()
由(2)得![]()
∴![]()
∴DE、DF、CF的长度之和不变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:5x﹣3x=( )
A.2x
B.2x2
C.﹣2x
D.﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在新年晚会的投飞镖游戏环节中,7名同学的投掷成绩(单位:环)分别是:7,9,9,4,9,8,8,则这组数据的众数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6cm,求CM和AD的长.

-
科目: 来源: 题型:
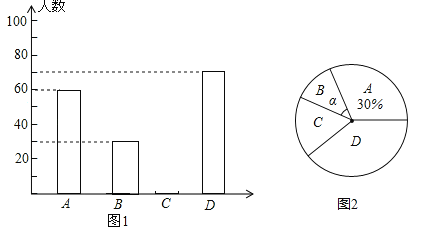
查看答案和解析>>【题目】黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题:
(1)本次抽样调查共抽取了多少名学生?并将条形统计图补充完整;
(2)本次抽样调查中,学习时间的中位数落在哪个等级内?
(3)表示B等级的扇形圆心角α的度数是多少?
(4)在此次问卷调查中,甲班有2人平均每天课外学习时间超过2小时,乙班有3人平均每天课外学习时间超过2小时,若从这5人中任选2人去参加座谈,试用列表或化树状图的方法求选出的2人来自不同班级的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句:①同一平面上,三条直线只有两个交点,则其中两条直线互相平行;②如果两条平行线被第三条截,同旁内角相等,那么这两条平行线都与第三条直线垂直;③过一点有且只有一条直线与已知直线平行,其中( )
A.①、②是正确的命题
B.②、③是正确命题
C.①、③是正确命题
D.以上结论皆错 -
科目: 来源: 题型:
查看答案和解析>>【题目】为拉动内需促进消费,某品牌的电视机经过两次降价,从原来每台6000元降到现在的每台4860元,求平均每次的降价率是多少?设每次降价率为x,由题意列方程为_____________________________.
相关试题

