【题目】已知二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①abc>0;②a﹣b+c<0;③2a+b﹣c<0;④4a+2b+c>0,⑤若点(﹣ ![]() ,y1)和(
,y1)和( ![]() ,y2)在该图象上,则y1>y2 . 其中正确的结论是(填入正确结论的序号)
,y2)在该图象上,则y1>y2 . 其中正确的结论是(填入正确结论的序号) 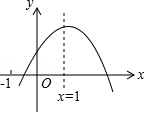
参考答案:
【答案】②③④
【解析】解:∵抛物线开口向下, ∴a<0,
∵对称轴在y轴右边,
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,
∴abc<0,故①错误;
∵二次函数y=ax2+bx+c图象可知,当x=﹣1时,y<0,
∴a﹣b+c<0,故②正确;
∵二次函数图象的对称轴是直线x=1,c>0,
∴﹣ ![]() =1,
=1,
∴2a+b=0,
∴2a+b<c,
∴2a+b﹣c<0,故③正确;
∵二次函数y=ax2+bx+c图象可知,当x=2时,y>0,
∴4a+2b+c>0,故④正确;
∵二次函数图象的对称轴是直线x=1,
∴抛物线上x=﹣ ![]() 时的点与当x=
时的点与当x= ![]() 时的点对称,
时的点对称,
∵x>1,y随x的增大而减小,
∴y1<y2 , 故⑤错误;
所以答案是:②③④.
【考点精析】利用二次函数图象以及系数a、b、c的关系对题目进行判断即可得到答案,需要熟知二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个长方形的长是
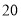 ,宽是,周长是
,宽是,周长是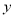 ,面积是
,面积是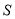 .
.(1)写出
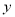 随
随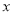 变化而变化的关系式;
变化而变化的关系式;(2)写出
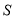 随
随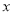 变化而变化的关系式;
变化而变化的关系式;(3)当
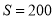 时,
时, 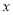 等于多少?
等于多少? 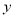 等于多少?
等于多少?(4)当
 增加
增加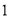 时,
时, 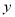 增加多少?
增加多少? 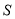 增加多少?
增加多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程或方程组解应用题:
从A地到B地有两条行车路线:
路线一:全程30千米,但路况不太好;
路线二:全程36千米,但路况比较好,
一般情况下走路线二的平均车速是走路线一的平均车速的1.8倍,走路线二所用的时间比走路线一所用的时间少20分钟.那么走路线二的平均车速是每小时多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】声音在空气中的传播速度v(m/s)与温度T(℃)的关系如下表:
温度/℃
0
5
10
15
20
速度v/(m/s)
331
334
337
340
343
(1)写出速度v与温度T之间的关系式;
(2)当T=30℃时,求声音的传播速度;
(3)当声音的传播速度为346m/s时,温度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“十一”黄金周期间,欢欢一家随旅游团到某风景区旅游,集体门票的收费标准是:
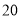 人以内(含
人以内(含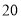 人),每人
人),每人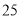 元;超过
元;超过 人的,超过的部分每人
人的,超过的部分每人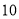 元.
元.(
 )写出应收门票费
)写出应收门票费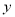 (元)与游览人数
(元)与游览人数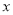 (人)(其中
(人)(其中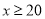 )之间的关系式.
)之间的关系式.(
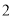 )利用(
)利用(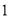 )中的关系式计算:若欢欢一家所在的旅游团共
)中的关系式计算:若欢欢一家所在的旅游团共 人,那么该旅游团购门票共花了多少钱?
人,那么该旅游团购门票共花了多少钱? -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下面两个定理:
①线段垂直平分线上的点到这条线段两个端点的距离相等;
②到一条线段两个端点距离相等的点在这条线段的垂直平分线上.
应用上述定理进行如下推理:
如图,直线l是线段MN的垂直平分线.

∵点A在直线l上,∴AM=AN.( )
∵BM=BN,∴点B在直线l上.( )
∵CM≠CN,∴点C不在直线l上.
这是∵如果点C在直线l上,那么CM=CN, ( )
这与条件CM≠CN矛盾.
以上推理中各括号内应注明的理由依次是 ( )
A. ②①① B. ②①②
C. ①②② D. ①②①
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,一张四边形纸片ABCD,∠A=50°,∠C=150°.若将其按照图②所示方式折叠后,恰好MD′∥AB,ND′∥BC,则∠D的度数为 .

相关试题

