【题目】如图,直线y=kx+6与x轴、y轴分别交于点E、F,点E的坐标为(﹣3,0),点A的坐标为(﹣2.5,0).
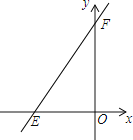
(1)求k的值;
(2)若点P(x,y)是第二象限内的直线上的一个动点,在点P的运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当点P运动到什么位置(求点P的坐标)时,△OPA的面积为5,并说明理由.
参考答案:
【答案】(1)k的值为2;(2)△OPA的面积S与x的函数关系式为S=2.5x+7.5(﹣3<x<0);(3)点P运动到(﹣1,4)或(﹣5,﹣4)时,△OPA的面积为5.
【解析】
试题分析:(1)由直线与x轴的交点的坐标,代入即可求出k的值;(2)过点P作x轴的垂线段,能够发现P点到x轴的距离为P点的纵坐标,代入直线方程用x表示出来P点的纵坐标,再套用三角形面积公式即可得出结论,再由点P在第二象限,即可确定x的取值范围;(3)分两种情况,一种P点在x轴上方,一种在x轴下方,分类讨论即可得出结论.
解:(1)∵点E(﹣3,0)在直线y=kx+6的图象上,
∴有0=﹣3k+6,解得:k=2.
故k的值为2.
(2)过点P作PB⊥x轴,垂足为点B,如图1.
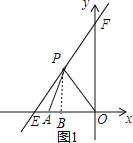
∵点P(x,y)是第二象限内的直线上的一个动点,
∴P点横坐标介于E、F的横坐标之间,
∴﹣3<x<0.
∵点P在直线y=2x+6上,
∴y=2x+6.
∵PB⊥x轴,且P点在第二象限,且点A的坐标为(﹣2.5,0),
∴PB=y=2x+6,OA=2.5.
∴△OPA的面积S=![]() OAPB=2.5x+7.5.
OAPB=2.5x+7.5.
故△OPA的面积S与x的函数关系式为S=2.5x+7.5(﹣3<x<0).
(3)∵令(2)中的关系式中x=0,解得S=7.5>5,
∴若点P在x轴上方时,必在第二象限,点P在x轴下方时,必在第三象限.
①当点P在x轴上方时,有△OPA的面积S=2.5x+7.5,
令S=5,即2.5x+7.5,解得:x=﹣1.
此时点P的坐标为(﹣1,4);
②当点P在x轴下方时,如图2,
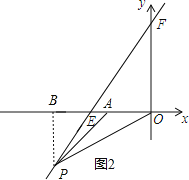
此时PB=﹣y=﹣2x﹣6,
△OPA的面积S=![]() OAPB=
OAPB=![]() ×2.5×(﹣2x﹣6)=﹣2.5x﹣7.5=5,
×2.5×(﹣2x﹣6)=﹣2.5x﹣7.5=5,
解得:x=﹣5.
此时点P的坐标为(﹣5,﹣4).
综上可知:点P运动到(﹣1,4)或(﹣5,﹣4)时,△OPA的面积为5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个三角形周长是15cm,其三条边长都是整数,则此三角形最长边最大值是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:a3÷a2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究与发现:RtΔABC中,∠C=90°,点D、E分别是ΔABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠
 .
.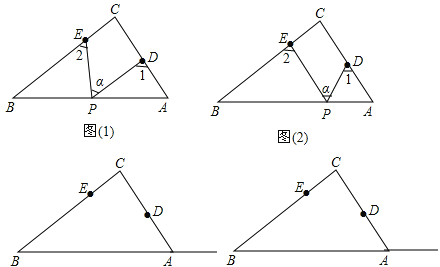
(1)若点P在线段AB上,如图(1)所示,且∠
 =50°,则∠1+∠2=___________;
=50°,则∠1+∠2=___________;(2)若点P在边AB上运动,如图(2)所示,则∠
 、∠1、∠2之间有何关系?
、∠1、∠2之间有何关系? (3)若点P在Rt△ABC斜边BA的延长线上运动(CE<CD),则∠
 、∠1、∠2之间有何关系?猜想并说明理由。
、∠1、∠2之间有何关系?猜想并说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个四边形的三个内角的度数依次如下选项,其中是平行四边形的是
A. 88°,108°,88°. B. 88°,104°,108°.
C. 88°,92°,92° . D. 88°,92°,88°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的两边长是3和4,周长是偶数,则这样的三角形的第三边是___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若三角形的三个外角的度数之比为2∶3∶4,则与之对应的三个内角的度数之比为( )
A. 4∶3∶2 B. 3∶2∶4 C. 5∶3∶1 D. 3∶1∶5
相关试题

