【题目】如图,在平行四边形ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F;点M是边AB的一个三等分点。则△AOE与△BMF的面积比为_________.

参考答案:
【答案】![]()
【解析】连接MF,作AG⊥BC交BC于点G,作MH⊥BC交BC于点H,
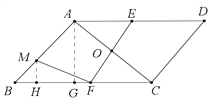
∵AB=AC,∴∠B=∠ACB=30°,
设AB=AC=6x,则BM=2x,
∴MH=BM·sin30°=x,AG=AB·sin30°=3x,BG=AB·cos30°=3![]() x,
x,
∵AB=AC,AG⊥BC,∴BG=CG=3![]() x,BC=6
x,BC=6![]() x,
x,
∵平行四边形ABCD,∴AD∥BC,OA=OC=3x,
∴∠EAO=∠ACB=30°,∴OE=OA·tan30°=![]() x,AE=
x,AE=![]() =2
=2![]() x,
x,
∴S△AOE=![]() OA·OE=
OA·OE=![]() x2,
x2,
∵在△AOE和△COF中,
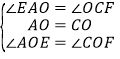 ,
,
∴△AOE≌△COF,
∴AE=CF=2![]() x,
x,
∴BF=6![]() x-2
x-2![]() x=4
x=4![]() x,
x,
∴S△BMF=![]() BF·MH=2
BF·MH=2![]() x2,
x2,
∴S△AOE∶S△BMF=(![]() x2)∶(2
x2)∶(2![]() x2)=3∶4.
x2)=3∶4.
故答案为3∶4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:
①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )

A. ②③ B. ②⑤ C. ①③④ D. ④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于
 MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(2,2)……根据这个规律,第25个点的坐标为____________,第2018个点的坐标为____________.
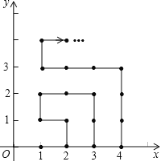
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节吃粽子是中华民族的传统习俗,五月初五早上,奶奶为小明准备了四只粽子:一只肉馅,一只香肠馅,两只红枣馅,四只粽子除内部馅料不同外其他均一切相同.小明喜欢吃红枣馅的粽子.
(1)请你用树状图为小明预测一下吃两只粽子刚好都是红枣馅的概率;
(2)在吃粽子之前,小明准备用一个均匀的正四面体骰子(如图所示)进行吃粽子的模拟试验,规定:掷得点数1向上代表肉馅,点数2向上代表香肠馅,点数3,4向上代表红枣馅,连续抛掷这个骰子两次表示随机吃两只粽子,从而估计吃两只粽子刚好都是红枣馅的概率.你认为这样模拟正确吗?试说明理由.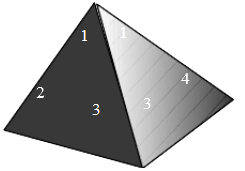
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,九年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.

(1)求共抽取了多少名学生的征文;
(2)将上面的条形统计图补充完整;
(3)在扇形统计图中,选择“爱国”主题所对应的圆心角是多少;
(4)如果该校九年级共有1200名学生,请估计选择以“友善”为主题的九年级学生有多少名.
相关试题

