【题目】如图,矩形![]() 中,
中,![]() ,
,![]() .点
.点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,点
上,点![]() 、
、![]() 在对角线
在对角线![]() 上.若四边形
上.若四边形![]() 是菱形,则
是菱形,则![]() 的长是( )
的长是( )

A. 2![]() B. 3
B. 3![]() C. 5 D. 6
C. 5 D. 6
参考答案:
【答案】C
【解析】
连接EF交AC于O,在矩形ABCD中,四边形EGFH是菱形,易证得△CFO≌△AOE,即可得OA=OC,然后由勾股定理求得AC的长,继而求得OA的长,又由△AOE∽△ABC,利用相似三角形的对应边成比例,即可求得答案.
连接EF交AC于O,
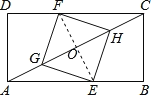
∵四边形EGFH是菱形,
∴EF⊥AC,OE=OF,
∵四边形ABCD是矩形,
∴∠B=∠D=90°,AB∥CD,
∴∠ACD=∠CAB,
在△CFO与△AOE中,
∠FCO=∠OAB,∠FOC=∠AOE,OF=OE,
∴△CFO≌△AOE(AAS),
∴AO=CO,
∵AC=![]() ,
,
∴AO=![]() AC=2
AC=2![]() ,
,
∵∠CAB=∠CAB,∠AOE=∠B=90°,
∴△AOE∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴AE=5.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某建筑工程队利用一面墙(墙的长度不限),用40米长的篱笆围成一个长方形的仓库.
(1)求长方形的面积是150平方米,求出长方形两邻边的长;
(2)能否围成面积220平方米的长方形?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM,下列结论:①AE=AF;②DF=DN;③AE=CN;④△AMD和△DMN的面积相等,其中错误的结论个数是( )

A.3个B.2个C.1个D.0个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,求旗杆的高度OM和玛丽在荡绳索过程中离地面的最低点的高度MN.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=40°,求∠D的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】
 中,
中, ,点
,点 为
为 三条角平分线的交点,
三条角平分线的交点, 于
于 ,
, 于
于 ,
, 于
于 ,且
,且 ,
, ,
, ,则点
,则点 到三边
到三边 、
、 、
、 的距离为( )
的距离为( )A. 2cm,2cm,2cm B. 3cm,3cm,3cm
C. 4cm,4cm,4cm D. 2cm,3cm,5cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】凸四边形
 的四个顶点满足:每一个顶点到其他三个顶点距离之积都相等.则四边形
的四个顶点满足:每一个顶点到其他三个顶点距离之积都相等.则四边形 一定是( )
一定是( )A. 正方形 B. 菱形 C. 等腰梯形 D. 矩形
相关试题

