搜索
【题目】a是整数，那么a2+a一定能被下面哪个数整除（ ）
A.2
B.3
C.4
D.5
参考答案：
【答案】A
【解析】解：∵a2+a=a（a+1），a是整数， ∴a（a+1）一定是两个连续的整数相乘，
∴a（a+1）一定能被2整除，
故选A．
【考点精析】根据题目的已知条件，利用因式分解的应用的相关知识可以得到问题的答案，需要掌握因式分解是整式乘法的逆向变形，可以应用与数字计算、求值、整除性问题、判断三角形的形状、解方程．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算（﹣3x2）3的结果是（ ）
A.9x5
B.﹣9x5
C.27x6
D.﹣27x6 -
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法正确的是（ ）
A.三点确定一个圆
B.一个三角形只有一个外接圆
C.和半径垂直的直线是圆的切线
D.三角形的内心到三角形三个顶点距离相等 -
科目： 来源： 题型：
查看答案和解析>>【题目】5a2b4-3ab2+ab3+7是_______次_________项式.
-
科目： 来源： 题型：
查看答案和解析>>【题目】李欣同学下午5：30放学离校，此刻时钟上时针与分针的夹角大小应为________ ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在平面直角坐标系中，△ABC是直角三角形,∠ACB=90,AC=BC,OA=1，OC=4，抛物线y=
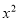+bx+c经过A，B两点，抛物线的顶点为D．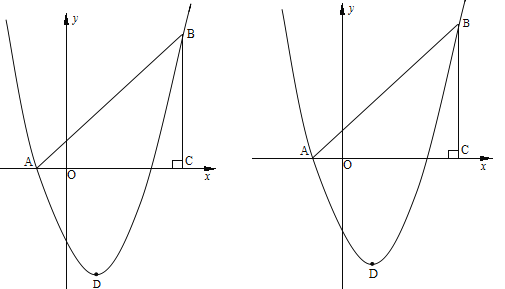
(1)、求b,c的值；
(2)、点E是直角三角形ABC斜边AB上一动点(点A、B除外)，过点E作x轴的垂线交抛物线于点F，当线段EF的长度最大时，求点E的坐标；
(3)、在（2）的条件下：①求以点E、B、F、D为顶点的四边形的面积；②在抛物线上是否存在一点P，使△EFP是以EF为直角边的直角三角形? 若存在，求出所有点P的坐标；若不存在，说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】画图并填空：如图，方格纸中每个小正方形的边长都为1．在方格纸中将△ABC经过一次平移后得到△A′B′C′，图中标出了点A、点B′、点C和它的对应点C′．
（1）请画出平移前后的△ABC和△A′B′C′；
（2）利用网格画出△ABC 中BC边上的中线AD；
（3）利用网格画出△ABC 中AB边上的高CE；
（4）△A′B′C′的面积为 .
相关试题
