【题目】某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中时间每增加1天,日销售量减少5件.
(1)第17天的日销售量是 件,日销售利润是 元.
(2)求试销售期间日销售利润的最大值.

参考答案:
【答案】(1)340;680(2)当x=18时,日销售利润最大,最大利润为720元
【解析】
(1)由图象可知第17天的日销售量为340件,根据日销售利润=每件的利润×日销售量,即可求出第17天的日销售利润;
(2)根据点的坐标,利用待定系数法可求出直线OD、DE的函数关系式,联立两函数关系式成方程组可求出点D的坐标,根据点D的坐标结合日销售利润=每件的利润×日销售量,即可求出日销售最大利润.
(1)由图可知:第17天的日销售量是340(件),(8﹣6)×340=680(元).
故答案为:340;680;
(2)设直线OD的函数关系式为y=kx+b,将(0,0)、(17,340)代入y=kx+b,![]() ,解得:
,解得:![]() ,∴直线OD的函数关系式为y=20x.
,∴直线OD的函数关系式为y=20x.
设直线DE的函数关系式为y=mx+n.
∵时间每增加1天,日销售量减少5件,∴当x=24时,y=340-(24-22)×5=330.将(22,340)、(24,330)代入y=mx+n,![]() ,解得:
,解得:![]() ,∴直线DE的函数关系式为y=﹣5x+450.
,∴直线DE的函数关系式为y=﹣5x+450.
联立两函数解析式成方程组,![]() ,解得:
,解得:![]() ,∴点D的坐标为(18,360).
,∴点D的坐标为(18,360).
∵折线ODE的最高点D的坐标为(18,360),360×2=720(元),∴当x=18时,日销售利润最大,最大利润为720元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如下表:
温度t/℃
…
﹣5
﹣3
2
…
植物高度增长量h/mm
…
34
46
41
…
科学家推测出h(mm)与t之间的关系可以近似地用二次函数来刻画.已知温度越适合,植物高度增长量越大,由此可以推测最适合这种植物生长的温度为( )
A. ﹣2℃ B. ﹣1℃ C. 0℃ D. 1℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示)
(I)根据图象,求一次函数y=kx+b的解析式,并写出自变量x的取值范围;
(Ⅱ)该公司要想每天获得最大的利润,应把销售单价定为多少?最大利润值为多少?

-
科目: 来源: 题型:
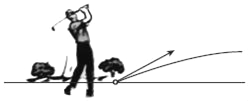
查看答案和解析>>【题目】如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.
(1)求小球飞行3s时的高度;
(2)问:小球的飞行高度能否达到22m?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解下列方程,其中应在方程左右两边同时加上4的是( )
A. x2﹣2x=5 B. x2+4x=5 C. 2x2﹣4x=5 D. 4x2+4x=5
-
科目: 来源: 题型:
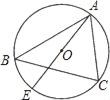
查看答案和解析>>【题目】如图,已知⊙O的直径AE=10cm,∠B=∠EAC,则AC的长为( )
A. 5cm B. 5
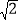 cm C. 5
cm C. 5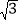 cm D. 6cm
cm D. 6cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②﹣1≤a≤﹣
 ;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

