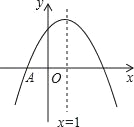
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②﹣1≤a≤﹣![]() ;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】D
【解析】
利用抛物线的开口方向可得a<0,再由抛物线的对称轴可得b=-2a,由此可对①进行判断;利用2≤c≤3结合已知条件可对②进行判断;利用二次函数的性质可对③进行判断;根据抛物线y=ax2+bx+c直线y=n-1的交点个数可对④进行判断.
∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=![]() =1,
=1,
∴b=-2a,
∴3a+b=3a-2a=a<0,故①正确;
∵抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),
∴a-b+c=0,∴c=-3a,
∵2≤c≤3,
∴2≤-3a≤3,
∴﹣1≤a≤﹣![]() ,故②正确;
,故②正确;
∵抛物线的顶点坐标为(1,n),
∴x=1时,二次函数有最大值为n,
∴对于任意实数m ,总有a+b+c≥am2+bm+c,
即a+b≥am2+bm,故③正确;
∵抛物线的顶点坐标为(1,n),
∴抛物线y=ax2+bx+c直线y=n-1有两个交点,
∴关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根,故④正确,
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中时间每增加1天,日销售量减少5件.
(1)第17天的日销售量是 件,日销售利润是 元.
(2)求试销售期间日销售利润的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解下列方程,其中应在方程左右两边同时加上4的是( )
A. x2﹣2x=5 B. x2+4x=5 C. 2x2﹣4x=5 D. 4x2+4x=5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的直径AE=10cm,∠B=∠EAC,则AC的长为( )
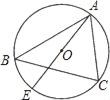
A. 5cm B. 5
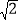 cm C. 5
cm C. 5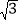 cm D. 6cm
cm D. 6cm -
科目: 来源: 题型:
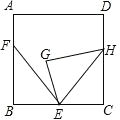
查看答案和解析>>【题目】如图,正方形 ABCD 中,点 E,F 分别在 BC 和 AB 上,BE=3,AF=2,BF=4,将△ BEF 绕点 E 顺时针旋转,得到△GEH,当点 H 落在 CD 边上时,F,H 两点之间的距离为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=4,D是线段BC上的一个动点,以AD为直径作⊙O分别交AB、AC于E、F,连结EF,则线段EF长度的最小值为_____.

-
科目: 来源: 题型:
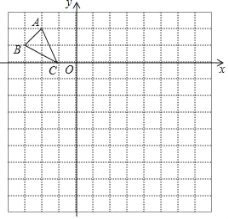
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的12×12网格中建立平面直角坐标系,格点△ABC(顶点是网格线的交点)的坐标分别是A(﹣2,2),B(﹣3,1),C(﹣1,0).
(1)将△ABC绕点O逆时针旋转90°得到△DEF,画出△DEF;
(2)以O为位似中心,将△ABC放大为原来的2倍,在网格内画出放大后的△A1B1C1,若P(x,y)为△ABC中的任意一点,这次变换后的对应点P1的坐标为 .
相关试题

