【题目】如图1是一张长方形的纸带,将这张纸带沿EF折叠成图2,再沿BF折叠成图3.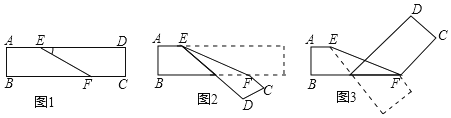
(1)若∠DEF=20°,请你求出图3中∠CFE度数;
(2)若∠DEF=a,请你直接用含a的式子表示图3中∠CFE的度数.
参考答案:
【答案】
(1)解:∵矩形对边AD∥BC,
∴CF∥DE,
∴图1中,∠CFE=180°﹣∠DEF=180°﹣20°=160°,
∵矩形对边AD∥BC,
∴∠BFE=∠DEF=20°,
∴图2中,∠BFC=160°﹣20°=140°,
由翻折的性质得,图3中∠CFE+∠BFE=∠BFC,
∴图3中,∠CFE+20°=140°,
∴图3中,∠CFE=120°
(2)解: 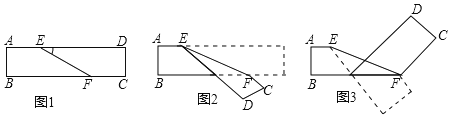
∵矩形对边AD∥BC,
∴CF∥DE,
∴图1中,∠CFE=180°﹣∠DEF=180°﹣a,
∵矩形对边AD∥BC,
∴∠BFE=∠DEF=a,
∴图2中,∠BFC=180°﹣2a,
由翻折的性质得,图3中∠CFE+∠BFE=∠BFC,
∴图3中,∠CFE+a=180°﹣2a,
∴图3中,∠CFE=180°﹣3a.
【解析】根据矩形的性质可解.
【考点精析】关于本题考查的平行线的性质,需要了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的多项式在实数范围内能因式分解的是( )
A.x2+y2
B.x2﹣y
C.x2+x+1
D.x2﹣2x+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)证明:“三角形内角和是180°”;
(2)请写出“直角三角形斜边上的中线等于斜边的一半”的逆命题,判断这一逆命题是真命题还是假命题,如果是真命题给出证明,如果是假命题,说明理由. -
科目: 来源: 题型:
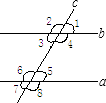
查看答案和解析>>【题目】如图所示,直线a、b被直线c所截,现给出下列四种条件:①∠2=∠6;②∠2=∠8;③∠1+∠4=180°;④∠3=∠8,其中能判断是a∥b的条件的序号是( )
A.①②
B.①③
C.①④
D.③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)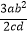
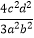
(2)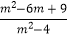
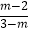
(3)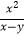 ﹣
﹣ 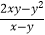
(4)x﹣y+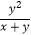 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,观测点A、旗杆DE的底端D、某楼房CB的底端C三点在一条直线上,从点A处测得楼顶端B的仰角为22°,此时点E恰好在AB上,从点D处测得楼顶端B的仰角为38.5°.已知旗杆DE的高度为12米,试求楼房CB的高度.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80)
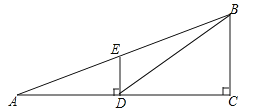
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的方程x2+mx+25=0有两个相等的实数根,那么m的值为_____.
相关试题

