Question

【题目】在等腰△ABC中，AB=AC，∠BAC=45°，CD是△ABC的高，P是线段AC（不包括端点A，C）上一动点，以DP为一腰，D为直角顶点（D、P、E三点逆时针）作等腰直角△DPE，连接AE．

（1）如图1，点P在运动过程中，∠EAD=______，写出PC和AE的数量关系；

（2）如图2，连接BE．如果AB=4，CP=，求出此时BE的长．

Answer 1

【答案】（1）45°；PC=AE，（2）.

【解析】

（1）根据全等三角形的性质即可得到结论；

（2）根据等腰直角三角形的性质得到∠DEP=∠DPE=45°，DE=DP．根据全等三角形的性质得到AE=PC=∠EAD=∠ACD=45°，过点E作EF⊥AB于F．根据勾股定理即可得到结论．

解：（1）PC=AE，

∵∠EDP=∠ADC=90°，

∴∠ADE+∠ADP=∠ADP+∠CDP=90°，

∴∠ADE=∠CDP，

在△ADE与△CDP中，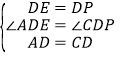

∴△ADE≌△CDP（SAS），

∴∠EAD=∠PCD=45°，PC=AE；

故答案为：45°；

（2）如图，

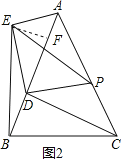
∵CD⊥AB，

∴∠ADC=90°．

∵∠BAC=45°，

∴AD=DC．

∵△DEP是等腰直角三角形，∠EDP=90°，

∴∠DEP=∠DPE=45°，DE=DP．

∵∠EDP=∠ADC=90°，

∴∠EDP-∠ADP=∠ADC-∠ADP．

∴∠EDA=∠PDC．

∴△EDA≌△PDC．（SAS），

∴AE=PC=∠EAD=∠ACD=45°，

过点E作EF⊥AB于F．

∴在Rt△AEF中，利用勾股定理，可得EF=AF=1，

∵AB=4，

∴BF=AB-AF=3．

∴BE==．