搜索
【题目】已知：如图，平行四边形ABCD 中，E、F 两点在对角线 BD 上，BE=DF．
(1) 求证：AE=CF；
(2) 当四边形AECF 为矩形时，直接写出
的值．
参考答案：
【答案】（1）证明见解析；（2）2.
【解析】（1）证明△ABE≌△CDF，根据全等三角形的对应边相等即可证得；（2）根据四边形AECF为矩形，矩形的对角线相等，则AC=EF，据此即可求解．
解：（1）如图所示，
∵ 四边形 ABCD 是平行四边形，
∴AB∥CD，AB=CD，
∴∠1=∠2
在△ABE 和△CDF 中，
AB=CD，∠1=∠2，BE=DF，
∴△ABE≌△CDF(SAS)
∴AE=CF．
（2） 当四边形 AECF 为矩形时， 
．
“点睛”此类试题属于难度较大的试题，考生解答此类试题时一定要把握好平行四边形的基本性质定理和判定定理，菱形的性质定理和判定定理，矩形的性质定理和判定定理．
-
科目： 来源： 题型：
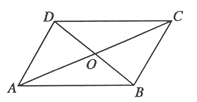
查看答案和解析>>【题目】如图，四边形ABCD中，AC，BD相交于点O，O是AC的中点，AD//BC，AC=8,BD=6.
（1）求证：四边形ABCD是平行四边形；
（2）若AC⊥BD，求□ABCD的面积.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，已知平行四边形ABCD，对角线AC，BD相交于点O，∠OBC=∠OCB．
（1）求证：平行四边形ABCD是矩形；
（2）请添加一个条件使矩形ABCD为正方形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将
ABCD的边AB延长到点E，使BE＝AB，连接DE，交边BC于点F．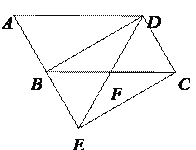
（1）求证：△BEF≌△CDF．
（2）连接BD，CE，若∠BFD＝2∠A，求证四边形BECD是矩形．
-
科目： 来源： 题型：
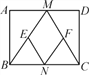
查看答案和解析>>【题目】如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点．
(1)求证：△ABM≌△DCM；
(2)当AB∶AD＝___时，四边形MENF是正方形，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F.
(1)求证：△AEF≌△DEB；
(2)求证：四边形ADCF是菱形；
(3)若AC＝4，AB＝5，求菱形ADCF的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在正方形ABCD中，AC是对角线，今有较大的直角三角板，一边始终经过点B，直角顶点P在射线AC上移动，另一边交DC于点Q.
(1)如图①，当点Q在DC边上时，猜想并写出PB与PQ所满足的数量关系，并加以证明；
(2)如图②，当点Q落在DC的延长线上时，猜想并写出PB与PQ满足的数量关系，并证明你的猜想．
相关试题
