【题目】如图l,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD、BC分别交于点E、F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G.
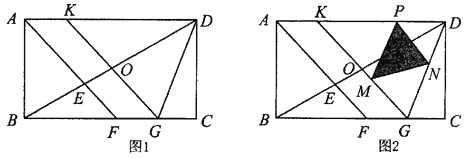
(1)求证:△DOK≌△BOG;
(2)求证:AB+AK=BG:
(3)如图2,若KD=KG=2,点P是线段KD上的动点(不与点D、K重台),PM∥DG交KG于点M,PN∥KG交DG于点N,设PD=x,S△PMN=y,求出y与x的函数关系式.
参考答案:
【答案】(1)证明见解析(2)![]()
【解析】(1)先根据AAS判定△DOK≌△BOG,(2)再根据等腰三角形ABF和平行四边形AFKG的性质,得出结论BG=AB+AK;(3)利用△DKG∽△PKM∽△DPN,由相似三角形的性质求出y与x的函数关系式.
解:(1)∵在矩形ABCD中,AD∥BC
∴∠KDO=∠GBO,∠DKO=∠BGO
∵点O是BD的中点
∴DO=BO
∴△DOK≌△BOG(AAS)
(2)∵四边形ABCD是矩形
∴∠BAD=∠ABC=90°,AD∥BC
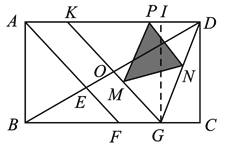
又∵AF平分∠BAD
∴∠BAF=∠BFA=45°
∴AB=BF
∵OK∥AF,AK∥FG
∴四边形AFGK是平行四边形
∴AK=FG
∵BG=BF+FG
∴BG=AB+AK
(3)解法一:
如图,过点G作GI⊥KD于点I,
由(2)知,四边形AFGK是平行四边形,△ABF为等腰直角三角形.
∴AF=KG=2, ![]() .
.
∵四边形ABCD是矩形,
∴GI=AB=![]() ,
,![]() 。
。
∵PD=x
∴PK=2﹣x
∵PM∥DG,PN∥KG
∴四边形PMGN是平行四边形,△DKG∽△PKM∽△DPN
∴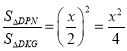 ,
,
即![]()
同理, ![]()
![]()
![]()
![]() .
.
解法二:
如图,过点P作PQ⊥KG于点Q,
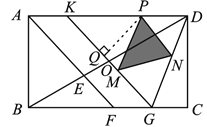
∴KD=KG,∠KDG=∠KGD
又∵PN∥KG
∴∠PND=∠KGD
∴∠PND=∠KDFG
∴PN=PD=x.
∵AF∥KG,
∴∠PKM=∠DAF=45°,又∵PK=2﹣x
∴![]()
又∵PN∥KG,
![]() .
.
“点睛”本题主要考查了矩形的性质以及平行四边形的性质,解题时需要运用全等三角形的判定与性质.解答此题的关键是运用相似三角形的面积之比等于相似比的平方这一性质,并根据图形面积的等量关系列出方程进行求解,难度较大,具有一定的综合性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠B=60',∠D=50°,将△CMN沿MN翻折得△EMN,若EM∥AB,EN∥AD,则∠C的度数为

A. 110° B. 115° C. 120° D. 125°
-
科目: 来源: 题型:
查看答案和解析>>【题目】“y与5的差比y的3倍多3”,由此可列出方程为______________.
-
科目: 来源: 题型:
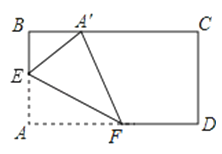
查看答案和解析>>【题目】如图,矩形纸片ABCD中,AB=6cm,AD=10cm,点E、F在矩形ABCD的边AB、AD上运动,将△AEF沿EF折叠,使点A′在BC边上,当折痕EF移动时,点A′在BC边上也随之移动.则A′C的取值范围为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定“中小学生每天在校体育活动时间不低于1小时”,为此,某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:
A组:t<0.5h;B组:0.5h≤t<1h;C组:1h≤t<1.5h;D组:t≥1.5h
请根据上述信息解答下列问题:
(1)C组的人数是,并补全直方图;
(2)本次调查数据的中位数落在哪组内?
(3)若该辖区约有24000名初中学生,请你估计其中达国家规定体育活动时间的人约有多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=5,P是BC边上除点B、C外的任意一点,则AP2+PBPC= .
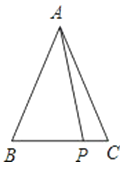
-
科目: 来源: 题型:
查看答案和解析>>【题目】新学期开学初,王刚同学对部分同学暑假在家做家务的时间进行了抽样调查(时间取整数小时),所得数据统计如下表:
时间分组
0.5~20.5
20.5~40.5
40.5~60.5
60.5~80.5
80.5~100.5
频 数
20
25
30
15
10
(1)王刚同学抽取样本的容量是多少?
(2)请你根据表中数据补全图中的频数分布直方图;
(3)若该学校有学生1260人,那么大约有多少学生在暑假做家务的时间在40.5~100.5小时之间?
相关试题

