搜索
【题目】设点A（﹣1，a）和点B（4，b）在直线y=﹣x+m上，则a与b的大小关系是（ ）
A.a=b
B.a＞b
C.a＜b
D.无法确定
参考答案：
【答案】B
【解析】解：因为k=﹣1＜0，
所以在函数y=﹣x+m中，y随x的增大而减小．
∵﹣1＜4，
∴a＞b．
故选B．
先判断出“k”的符号，再根据一次函数的性质判断出a、b的大小．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们规定：将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“面线”，“面线”被这个平面图形截得的线段叫做该图形的“面径”（例如圆的直径就是它的“面径”）．已知等边三角形的边长为4，则它的“面径”长x的取值范围是 _.
-
科目： 来源： 题型：
查看答案和解析>>【题目】若正整数n使得在计算n+（n+1）+（n+2）的过程中，个数位上均不产生进为现象，则称n为“本位数”，例如2和30是“本位数”，而5和91不是“本位数”.现从所有大于0且小于100的“本位数”中，随机抽取一个数，抽到奇数的概率为 .
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了美化校园环境，加大校园绿化投资．某区前年用于绿化的投资为18万元，今年用于绿化的投资为33万元，设这两年用于绿化投资的年平均增长率为x，则（ ）
A.18（1+2x）＝33B.18（1+x2）＝33
C.18（1+x）2＝33D.18（1+x）+18（1+x）2＝33
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE。
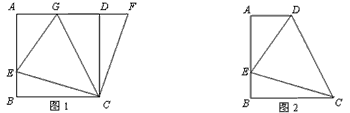
（1）求证：CE=CF；
（2）在图1中，若G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？
（3）运用（1）（2）解答中所积累的经验和知识，完成下题：
如图2，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B=90°，AB=BC=12，E是AB上一点，且
∠DCE=45°，BE=4，求DE的长。 -
科目： 来源： 题型：
查看答案和解析>>【题目】将两张宽度相等的矩形纸片叠放在一起得到如图所示的四边形ABCD.
（1）求证：四边形ABCD是菱形；
（2）如果两张矩形纸片的长都是8，宽都是2．那么△DCB的面积是否存在最大值或最小值？如果存在，请求出来；如果不存在，请简要说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）计算：
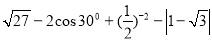；（2）解不等式：
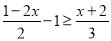并将解集在数轴上表示出来.
相关试题
