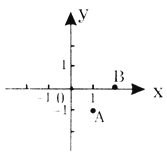
【题目】如图,在平面直角坐标系中,以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形第四个顶点坐标的是
( )
A.(3,-1)
B.(-1,-1)
C.(1,1)
D.(-2,-1)
参考答案:
【答案】D
【解析】
根据以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,根据平行四边形的判定分别对答案A,B,C,D进行分析即可得出符合要求的答案.
A、∵以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,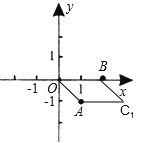
当第四个点为(3,-1)时,
∴BO=AC1=2,
∵A,C1 , 两点纵坐标相等,
∴BO∥AC1 ,
∴四边形OAC1B是平行四边形;故此选项正确;
B、∵以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,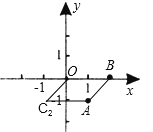
当第四个点为(-1,-1)时,
∴BO=AC2=2,
∵A,C2 , 两点纵坐标相等,
∴BO∥AC2 ,
∴四边形OC2AB是平行四边形;故此选项正确;
C、∵以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,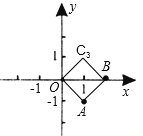
当第四个点为(1,1)时,
∴BO=AC1=2,
∵A,C1 , 两点纵坐标相等,
∴C3O=BC3=![]() ,
,
同理可得出AO=AB=![]() ,
,
进而得出C3O=BC3=AO=AB,∠OAB=90°,
∴四边形OABC3是正方形;故此选项正确;
D、∵以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,
当第四个点为(-1,-1)时,四边形OC2AB是平行四边形;
∴当第四个点为(-2,-1)时,四边形OC2AB不可能是平行四边形;
故此选项错误.
故选D.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E为BC的中点,AE与对角线BD交于点F.
(1)求证:DF=2BF;
(2)当∠AFB=90°且tan∠ABD=
 时, 若CD=
时, 若CD= ,求AD长.
,求AD长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2﹣4x+4= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,点P(-3,-5)关于原点对称点的坐标是( )
A.(3,5)B.(5,3)C.(-5,-3)D.(3,-5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,y不是x的函数的是( )
A. y=|x| B. y=x C. y=﹣x+1 D. y=±x
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,两对角线交于点O,则图中面积相等的三角形有( ).

A.4对
B.3对
C.2对
D.1对 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,给出如下定义:
对于⊙C及⊙C外一点P,M,N是⊙C上两点,当∠MPN最大时,称∠MPN为点P关于⊙C的“视角”.
(1)如图,⊙O的半径为1,
①已知点A(0,2),画出点A关于⊙O的“视角”;
若点P在直线x = 2上,则点P关于⊙O的最大“视角”的度数 ;
②在第一象限内有一点B(m,m),点B关于⊙O的“视角”为60°,求点B的坐标;
③若点P在直线
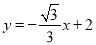 上,且点P关于⊙O的“视角”大于60°,求点P的横坐标
上,且点P关于⊙O的“视角”大于60°,求点P的横坐标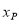 的取值范围.
的取值范围.(2)⊙C的圆心在x轴上,半径为1,点E的坐标为(0,1),点F的坐标为(0,-1),若线段EF上所有的点关于⊙C的“视角”都小于120°,直接写出点C的横坐标
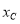 的取值范围.
的取值范围.
相关试题

