【题目】通过对《勾股定理》的学习,我们知道:如果一个三角形中,两边的平方和等于第三边的平方,那么这个三角形一定是直角三角形.如果我们新定义一种三角形——两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形.
(1)根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗?
(填“是”或不是);
(2)若某三角形的三边长分别为1、![]() 、2,则该三角形是不是奇异三角形,请做出判断并写出判断依据;
、2,则该三角形是不是奇异三角形,请做出判断并写出判断依据;
(3)在![]() 中,两边长分别为
中,两边长分别为![]() ,且且
,且且![]() ,则这个三角形是不是奇异三角形?请做出判断并写出判断依据;
,则这个三角形是不是奇异三角形?请做出判断并写出判断依据;
探究:Rt![]() 中,
中,![]() ,且b>a,若Rt
,且b>a,若Rt![]() 是奇异三角形,求
是奇异三角形,求![]() .
.
参考答案:
【答案】(1)是;(2)是奇异三角形;(3) 是,见解析;拓展: ![]()
【解析】
(1)根据“奇异三角形”的定义与等边三角形的性质,求证即可;(2)根据“奇异三角形”的定义问题可解;(3)通过分类讨论,分别验证即可;探究:先根据勾股定理得出Rt△ABC各边之间的关系,再根据此三角形是奇异三角形可用a表示出b、c的值,即可得出结果.
解:(1)是;设等边三角形的一边为a,则a2+a2=2a2,
∴符合奇异三角形”的定义.
∴正确;
(2)![]()
![]() 该三角形一定是奇异三角形
该三角形一定是奇异三角形
(3)![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
探究:![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,已知正方形ABCD,E是AD上一点,F是BC上一点,G是AB上一点,H是CD上一点,线段EF、GH交于点O,∠EOH=∠C,求证:EF=GH;
(2)如图2,若将“正方形ABCD”改为“菱形ABCD”,其他条件不变,探索线段EF与线段GH的关系并加以证明;
(3)如图3,若将“正方形ABCD”改为“矩形ABCD”,且AD=mAB,其他条件不变,探索线段EF与线段GH的关系并加以证明;

附加题:根据前面的探究,你能否将本题推广到一般的平行四边形情况?若能,写出推广命题,画出图形,并证明,若不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
, ,
, ,以斜边
,以斜边 的中点
的中点 为旋转中心,把这个三角形按逆时针方向旋转
为旋转中心,把这个三角形按逆时针方向旋转 得到
得到 ,则旋转后两个直角三角形重叠部分的面积为( )
,则旋转后两个直角三角形重叠部分的面积为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1是一个重要公式的几何解释.请你写出这个公式: ;
(2)如图2,已知
 ,
, ,且
,且 三点共线.
三点共线.试证明
 ;
;
(3)勾股定理是几何学中的明珠,千百年来,人们对它的证明趋之若骛,有资料表明,关于勾股定理的证明方法已有500余种.课本中介绍了比较有代表性的赵爽弦图.
伽菲尔德(Garfield,1881年任美国第20届总统)利用图2证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),请你写出该证明过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,四边形
 各个顶点坐标分别为
各个顶点坐标分别为 ,
, ,
, .
. 画出平面直角坐标系,并画四边形
画出平面直角坐标系,并画四边形 .
. 试确定图中四边形
试确定图中四边形 的面积.
的面积. 如果将四边形
如果将四边形 绕点
绕点 旋转
旋转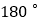 ,试确定旋转后四边形上各个顶点的坐标.
,试确定旋转后四边形上各个顶点的坐标. 如果
如果 ,你能重新建立适当的坐标系,横坐标乘以
,你能重新建立适当的坐标系,横坐标乘以 得的图形与原图形重合吗?请说明理由.
得的图形与原图形重合吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 与
与 是两个大小不同的等腰直角三角形.
是两个大小不同的等腰直角三角形. 如图①所示,连接
如图①所示,连接 ,
, ,试判断线段
,试判断线段 和
和 的数量和位置关系,并说明理由;
的数量和位置关系,并说明理由; 如图②所示,连接
如图②所示,连接 ,将线段
,将线段 绕
绕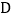 点顺时针旋转
点顺时针旋转 到
到 ,连接
,连接 ,试判断线段
,试判断线段 和
和 的数量和位置关系,并说明理由.
的数量和位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=BC,将△ABC绕点B顺时针旋转α度,得到△A1BC1,A1B交AC于E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF=α,②A1E=CF,③DF=FC,④AD=CE,⑤A1F=CE.其中一定正确的有
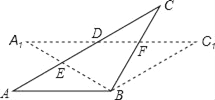
A. ①②④ B. ②③④ C. ①②⑤ D. ③④⑤
相关试题

