【题目】(1)如图1是一个重要公式的几何解释.请你写出这个公式: ;
(2)如图2,已知![]() ,
,![]() ,且
,且![]() 三点共线.
三点共线.
试证明![]() ;
;

(3)勾股定理是几何学中的明珠,千百年来,人们对它的证明趋之若骛,有资料表明,关于勾股定理的证明方法已有500余种.课本中介绍了比较有代表性的赵爽弦图.
伽菲尔德(Garfield,1881年任美国第20届总统)利用图2证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),请你写出该证明过程.
参考答案:
【答案】⑴ ![]() .⑵见解析;⑶见解析;
.⑵见解析;⑶见解析;
【解析】
(1)由大正方形面积的两种计算方法即可得出结果;
(2)由全等三角形的性质得出∠BAC=∠DCE,再由角的互余关系得出∠ACB+∠DCE=90°,即可得出结论;
(3)梯形ABDE的面积用两种计算方法即可得出结论.
⑴ 这个公式为![]() .
.
⑵ ∵![]() ,∴
,∴![]() .
.
![]() .
.
由于点![]() 共线,
共线,
所以![]() .
.
⑶ 梯形![]() 的面积为
的面积为
![]() ;
;
另一方面,梯形![]() 可分成三个直角三角形,其面积又可以表示成
可分成三个直角三角形,其面积又可以表示成![]()
∴![]() ,即
,即![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国北京已获得2022年第24届冬季奥林匹克运动会举办权,北京也将创造历史,成为第一个既举办过夏奥会又举办冬奥会的城市.张家口也成为本届冬奥会的协办城市,为此,中国设计了第一条采用我国自主研发的北斗卫星导航系统的智能化高速铁路——京张高铁,作为2022年北京冬奥会重要交通保障设施.已知北京至张家口铁路,铁路全长约180千米.按照设计,京张高铁列车的平均行驶速度是普通快车的1.5倍,用时比普通快车用时少了20分钟,求高铁列车的平均行驶速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,已知正方形ABCD,E是AD上一点,F是BC上一点,G是AB上一点,H是CD上一点,线段EF、GH交于点O,∠EOH=∠C,求证:EF=GH;
(2)如图2,若将“正方形ABCD”改为“菱形ABCD”,其他条件不变,探索线段EF与线段GH的关系并加以证明;
(3)如图3,若将“正方形ABCD”改为“矩形ABCD”,且AD=mAB,其他条件不变,探索线段EF与线段GH的关系并加以证明;

附加题:根据前面的探究,你能否将本题推广到一般的平行四边形情况?若能,写出推广命题,画出图形,并证明,若不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
, ,
, ,以斜边
,以斜边 的中点
的中点 为旋转中心,把这个三角形按逆时针方向旋转
为旋转中心,把这个三角形按逆时针方向旋转 得到
得到 ,则旋转后两个直角三角形重叠部分的面积为( )
,则旋转后两个直角三角形重叠部分的面积为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】通过对《勾股定理》的学习,我们知道:如果一个三角形中,两边的平方和等于第三边的平方,那么这个三角形一定是直角三角形.如果我们新定义一种三角形——两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形.
(1)根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗?
(填“是”或不是);
(2)若某三角形的三边长分别为1、
 、2,则该三角形是不是奇异三角形,请做出判断并写出判断依据;
、2,则该三角形是不是奇异三角形,请做出判断并写出判断依据;(3)在
 中,两边长分别为
中,两边长分别为 ,且且
,且且 ,则这个三角形是不是奇异三角形?请做出判断并写出判断依据;
,则这个三角形是不是奇异三角形?请做出判断并写出判断依据;探究:Rt
 中,
中, ,且b>a,若Rt
,且b>a,若Rt 是奇异三角形,求
是奇异三角形,求 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,四边形
 各个顶点坐标分别为
各个顶点坐标分别为 ,
, ,
, .
. 画出平面直角坐标系,并画四边形
画出平面直角坐标系,并画四边形 .
. 试确定图中四边形
试确定图中四边形 的面积.
的面积. 如果将四边形
如果将四边形 绕点
绕点 旋转
旋转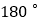 ,试确定旋转后四边形上各个顶点的坐标.
,试确定旋转后四边形上各个顶点的坐标. 如果
如果 ,你能重新建立适当的坐标系,横坐标乘以
,你能重新建立适当的坐标系,横坐标乘以 得的图形与原图形重合吗?请说明理由.
得的图形与原图形重合吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 与
与 是两个大小不同的等腰直角三角形.
是两个大小不同的等腰直角三角形. 如图①所示,连接
如图①所示,连接 ,
, ,试判断线段
,试判断线段 和
和 的数量和位置关系,并说明理由;
的数量和位置关系,并说明理由; 如图②所示,连接
如图②所示,连接 ,将线段
,将线段 绕
绕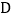 点顺时针旋转
点顺时针旋转 到
到 ,连接
,连接 ,试判断线段
,试判断线段 和
和 的数量和位置关系,并说明理由.
的数量和位置关系,并说明理由.
相关试题

