【题目】探索规律:
 观察由※组成的图案和算式,解答问题:
观察由※组成的图案和算式,解答问题:
1+3=4=![]()
1+3+5=9=![]()
1+3+5+7=16=![]()
1+3+5+7+9=25=![]()
(1)请猜想1+3+5+7+9+ … +29= ;(3分)
(2)请猜想1+3+5+7+9+ … +(2n-1)+(2n+1)= ;(3分)
(3)请用上述规律计算:(6分)41+43+45+ …… +77+79
参考答案:
【答案】(1)、225;(2)、![]() ;(3)、1200
;(3)、1200
【解析】
试题分析:(1)、根据题意可得规律为:从1开始的连续的奇数的和等于奇数的个数的平方;(2)、根据这一规律然后进行计算求解;(3)、将原式转化为(1+3+5+7+……+39+41+43+……+79)-(1+3+5+7+……+39),然后根据规律进行计算.
试题解析:(1)、原式=![]() =225;
=225;
(2)、![]()
(3)、原式=(1+3+5+7+……+39+41+43+……+79)-(1+3+5+7+……+39)=![]() =1600-400=1200
=1600-400=1200
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正方体的体积是1 000 cm3,现在要在它的8个角上分别截去8个大小相同的小正方体,使得截去后余下的体积是488 cm3,问截得的每个小正方体的棱长是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某书店把一本新书按标价的九折出售,仍可获利 20%.若该书的进价为 21 元,则标价为______元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(0,1),C(4,3),E
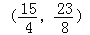 ,P是以AC为对角线的矩形ABCD内部(不在各边上)的一动点,点D在y轴上,抛物线y=ax2+bx+1以P为顶点.
,P是以AC为对角线的矩形ABCD内部(不在各边上)的一动点,点D在y轴上,抛物线y=ax2+bx+1以P为顶点.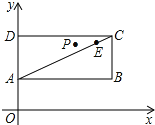
(1)求证:A、C、E三点共线;
(2)设抛物线y=ax2+bx+1与x轴有交点F、G(F在G的左侧),△GAO与△FAO的面积差为3,且这条抛物线与线段AE有两个不同的交点,试确定a、b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,BC=15,AC=20,CD是高.
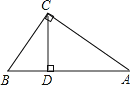
(1)求AB的长;
(2)求△ABC的面积;
(3)求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简后求值 2(x2y+xy2)﹣2(x2y﹣3x)﹣2xy2﹣2y的值,其中x=﹣1,y=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行线判定:在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线也_______________.
相关试题

