Question

【题目】我们运用图（Ⅰ）中大正方形的面积可表示为（a+b）2 ， 也可表示为c3+4（ab），即（a+b）2=c2+4（ab）由此推导出一个重要的结论a2+b2=c2 ， 这个重要的结论就是著名的“勾股定理”．这种根据图形可以极简单地直观推论或验证数学规律和公式的方法，简称“无字证明”．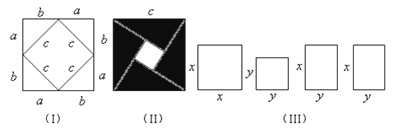

（1）请你用图（Ⅱ）（2002年国际数学家大会会标）的面积表达式验证勾股定理（其中四个直角三角形的较大的直角边长都为a，较小的直角边长都为b，斜边长都为c）．
（2）请你用（Ⅲ）提供的图形进行组合，用组合图形的面积表达式验证：（x+2y）2=x2+4xy+4y2 ．

Answer 1

【答案】解：（1）S阴影=4×ab，S阴影=c2﹣（a﹣b）2 ，
∴4×ab=c2﹣（a﹣b）2 ， 即2ab=c2﹣a2+2ab﹣b2 ，
则a2+b2=c2；
（2）如图所示，

大正方形的面积为x2+4y2+4xy，也可以为（x+2y）2 ，
则（x+2y）2=x2+4xy+4y2 ．
【解析】（1）阴影部分面积由大正方形面积减去小正方形面积，也可以由四个直角三角形面积之和求出，两者相等即可得证；
（2）拼成如图所示图形，根据大正方形边长为x+2y，表示出正方形面积，再由两个小正方形与两个矩形面积之和求出，即可验证．