【题目】下列说法正确的是( ) ①试验条件不会影响某事件出现的频率;
②在相同的条件下试验次数越多,就越有可能得到较精确的估计值,但各人所得的值不一定相同;
③如果一枚骰子的质量分布均匀,那么抛掷后每个点数出现的机会均等;
④抛掷两枚质量分布均匀的相同的硬币,出现“两个正面”、“两个反面”、“一正一反”的机会相同.
A.①②
B.②③
C.③④
D.①③
参考答案:
【答案】B
【解析】解:①错误,实验条件会极大影响某事件出现的频率;②正确;③正确;④错误,“两个正面”、“两个反面”的概率为 ![]() ,“一正一反”的机会较大,为
,“一正一反”的机会较大,为 ![]() .
.
故选B.
【考点精析】关于本题考查的可能性的大小和概率的意义,需要了解一般地,随机事件发生的可能性是有大小的,不同的随机事件发生的可能性的大小有可能不同;任何事件的概率是0~1之间的一个确定的数,它度量该事情发生的可能性.小概率事件很少发生,而大概率事件则经常发生.知道随机事件的概率有利于我们作出正确的决策才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验室里,水平桌面上有甲、乙两个圆柱形容器(容器足够高),底面半径之比为1∶2,用一个管子在甲、乙两个容器的15厘米高度处连通(即管子底端离容器底15厘米).已知只有乙容器中有水,水位高2厘米,如图所示.现同时向甲、乙两个容器注水,平均每分钟注入乙容器的水量是注入甲容器水量的k倍.开始注水1分钟,甲容器的水位上升a厘米,且比乙容器的水位低1厘米.其中a,k均为正整数,当甲、乙两个容器的水位都到达连通管子的位置时,停止注水.甲容器的水位有2次比乙容器的水位高1厘米,设注水时间为t分钟.

(1)求k的值(用含a的代数式表示).
(2)当甲容器的水位第一次比乙容器的水位高1厘米时,求t的值.
(3)当甲容器的水位第二次比乙容器的水位高1厘米时,求a,k,t的值.
-
科目: 来源: 题型:
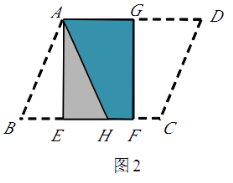
查看答案和解析>>【题目】(本题10分) 如图1,将△ABC纸片沿中位线EH折叠,使点A的对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形.类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩 形,这样的矩形称为叠合矩形.
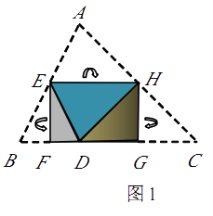

(1)将□ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段 , ;S矩形AEFG:S□ABCD=
(2)ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH,若EF=5,EH=12,求AD的长.
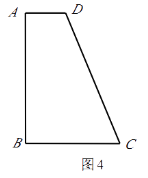
(3)如图4,四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC,AB=8,CD=10.小明把该纸片折叠,得到叠合正方形.请你帮助画出叠合正方形的示意图,并求出AD,BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某个图形是按下面方法连接而成的:(0,0)→(2,0);(1,0)→(0,﹣1);(1,1)→(1,﹣2);(1,0)→(2,﹣1).
(1)请连接图案,它是一个什么汉字?
(2)作出这个图案关于y轴的轴对称图形,并写出新图案相应各端点的坐标,你得到一个什么汉字?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有小正方形的边长都为1,A、B、C都在格点上.
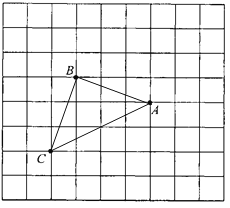
(1)过点B画直线AC的垂线,并注明垂足为G;
(2)线段 的长度是点B到直线AC的距离;
线段BC的长度是点 到直线 的距离;
(3)因为直线外一点与直线上各点连接的所有线段中,垂线段最短,所以线段BC、BG的大小关系为:BC BG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某收费站在2小时内对经过该站的机动车统计如下:
类型
轿车
货车
客车
其他
数量(辆)
36
24
8
12
若有一辆机动车将经过这个收费站,利用上面的统计估计它是轿车的概率为( )
A.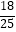
B.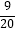
C.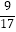
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.
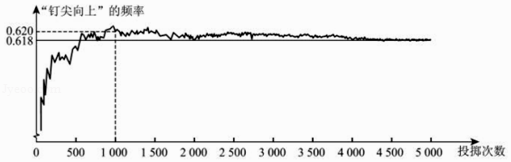
下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A.①
B.②
C.①②
D.①③
相关试题

