【题目】如图,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 在
在![]() 上从
上从![]() 向
向![]() 运动,连接
运动,连接![]() 交
交![]() 于点
于点![]() .
.
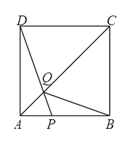
(![]() )试证明:无论点
)试证明:无论点![]() 运动到
运动到![]() 上何处时,都有
上何处时,都有![]() ≌
≌![]() .
.
(![]() )若点
)若点![]() 从点
从点![]() 运动到点
运动到点![]() ,再继续在
,再继续在![]() 上运动到点
上运动到点![]() ,在整个运动过程中,当点
,在整个运动过程中,当点![]() 运动到什么位置时,
运动到什么位置时, ![]() 恰为等腰三角形.
恰为等腰三角形.
参考答案:
【答案】(![]() )证明见解析;(
)证明见解析;(![]() )
)![]() 。
。
【解析】分析:(1)根据正方形的四条边都相等可得AD=AB,对角线平分一组对角可得∠DAQ=∠BAQ=45°,然后利用“边角边”证明△ADQ和△ABQ全等;(2)分①AQ=DQ时,点B、P重合,②AQ=AD时,根据等边对等角可得∠ADQ=∠AQD,再求出正方形的对角线AC的长,再求出CQ,然后根根据两直线平行,内错角相等求出∠CPQ=∠ADQ,从而得到∠CQP=∠CPQ,根据等角对等边可得CP=CQ,从而得到点P的位置,③AD=DQ时,点C、P、Q三点重合.
本题解析:
(![]() )如图,∵在正方形
)如图,∵在正方形![]() 中,无论
中,无论![]() 运动到
运动到![]() 何处,
何处,
都有![]() ,
, ![]() .
.
∴在![]() 和
和![]() 中,
中, 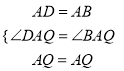 .
.
∴![]() ≌
≌![]() .
.
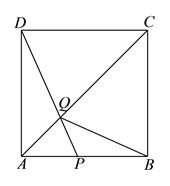
(![]() )
)![]() 为等腰三角形.
为等腰三角形.
如图, ![]() 时,此时
时,此时![]() 为正方形.
为正方形.
![]() 的中心,此时点
的中心,此时点![]() 与点
与点![]() 重合.
重合.
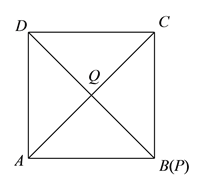
②如图, ![]() 时,由等边对等角得:
时,由等边对等角得: ![]() .
.
∴![]() ,
, ![]() .
.
∴![]()
∵![]()
∵![]()
∴![]()
∴![]() .
.
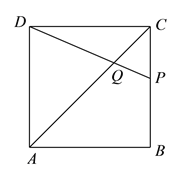
③如图, ![]() 时,
时,
此时![]() 、
、![]() 、
、![]() 三点重合.
三点重合.
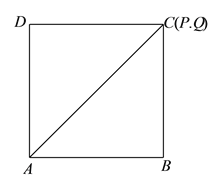
综上所述:当![]() 运动到①
运动到①![]() 点位置②
点位置②![]() 处(
处(![]() 上)③
上)③![]() 点位置时,
点位置时, ![]() 为等腰三角形.
为等腰三角形.
-
科目: 来源: 题型:
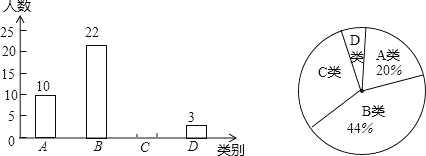
查看答案和解析>>【题目】某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试,并按测试成绩(单位:分)分成四类:A类(12≤m≤15),B类(9≤m≤11),C类(6≤m≤8),D类(m≤5)绘制出以下两幅不完整的统计图,请根据图中信息解答下列问题:
(1)本次抽取样本容量为 ,扇形统计图中A类所对的圆心角是 度;
(2)请补全统计图;
(3)若该校九年级男生有300名,请估计该校九年级男生“引体向上”项目成绩为C类的有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(-2,a)和点B(b,-5)关于x轴对称,则a+b=___________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次知识竞赛共有20道选择题,规定答对一道题得5分,不做或做错一题扣1分,如果某学生的得分为76分,则他做对了道题( )
A. 16 B. 17 C. 18 D. 19
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:3(x2﹣2xy)﹣(2x2﹣xy),其中x=2,y=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个三角形的两边长分别为5,12,则第三边的长可以是( )
A.18
B.13
C.7
D.5 -
科目: 来源: 题型:
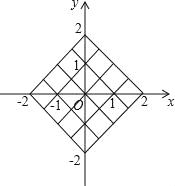
查看答案和解析>>【题目】在一个不透明的布袋中装有三个小球,小球上分别标有数字﹣1、0、2,它们除了数字不同外,其他都完全相同.
(1)随机地从布袋中摸出一个小球,则摸出的球为标有数字2的小球的概率为 ;
(2)小丽先从布袋中随机摸出一个小球,记下数字作为平面直角坐标系内点M的横坐标.再将此球放回、搅匀,然后由小华再从布袋中随机摸出一个小球,记下数字作为平面直角坐标系内点M的纵坐标,请用树状图或表格列出点M所有可能的坐标,并求出点M落在如图所示的正方形网格内(包括边界)的概率.
相关试题

