【题目】小东从甲地出发匀速前往相距20km的乙地,一段时间后,小明从乙地出发沿同一条路匀速前往甲地.小东出发2.5h后,在距乙地7.5km处与小明相遇,之后两人同时到达终点.图中线段AB、CD分别表示小东、小明与乙地的距离y(km)与小东所用时间x(h)的关系.
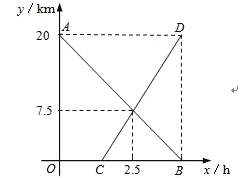
(1)求线段AB、CD所表示的y与x之间的函数表达式;
(2)小东出发多长时间后,两人相距16km?
参考答案:
【答案】(1)线段AB所表示的y与x之间的函数表达式为y1=﹣5x+20;
线段CD所表示的y与x之间的函数表达式为:y2=![]() x﹣
x﹣![]() ;
;
(2)小东出发0.8h或3.7h后,两人相距16km.
【解析】
试题分析:(1)分别利用A,B和(2.5,7.5),D点坐标求出函数解析式得出答案;
(2)利用①当0≤x<1.6时,②当1.6≤x<2.5时,y1﹣y2=16,③当2.5≤x≤4时,分别得出x的值进而得出答案.
试题解析:(1)设线段AB所表示的y与x之间的函数表达式为y1=kx+b,
由图象可知,函数图象经过点(0,20)、(2.5,7.5).
得![]() ,
,
解得:![]() ,
,
所以线段AB所表示的y与x之间的函数表达式为y1=﹣5x+20.
令y1=0,得x=4.
所以B点的坐标为(4,0).所以D点的坐标为(4,20).
设线段CD所表示的y与x之间的函数表达式为y2=mx+n,
因为函数图象经过点(4,20)、(2.5,7.5).
得![]() ,
,
解得: ,
,
所以线段CD所表示的y与x之间的函数表达式为:y2=![]() x﹣
x﹣![]() ;
;
(2)线段CD所表示的y与x之间的函数表达式为y2=![]() x﹣
x﹣![]() ,
,
令y2=0,得x=1.6.即小东出发1.6 h后,小明开始出发.
①当0≤x<1.6时,y1=16,即﹣5x+20=16,
解得:x=0.8,
②当1.6≤x<2.5时,y1﹣y2=16,即﹣5x+20﹣(![]() x﹣
x﹣![]() )=16,
)=16,
解得:x=1.3(舍去)
③当2.5≤x≤4时,y2﹣y1=16,即![]() x﹣
x﹣![]() ﹣(﹣5x+20)=16,
﹣(﹣5x+20)=16,
解得:x=3.7.
答:小东出发0.8h或3.7h后,两人相距16km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区冬季最高气温为零下 1℃,最低零下 17℃,日均最高气温比最低气温高( )
A. 16℃ B. 17℃ C. 18℃ D. 19℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE.
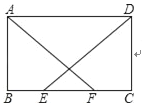
求证:(1)△ABF≌△DCE;
(2)四边形ABCD是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某一时刻太阳光从教室窗户射入室内,与地面的夹角∠BPC为30°,窗户的一部分在教室地面所形成的影长PE为3.5米,窗户的高度AF为2.5米.求窗外遮阳蓬外端一点D到教室窗户上椽的距离AD.(结果精确0.1米)
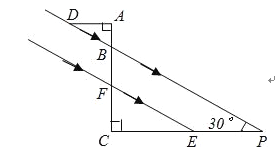
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形BCDE的各边分别平行于
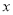 轴或
轴或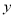 轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2015次相遇地点的坐标
轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2015次相遇地点的坐标是( )
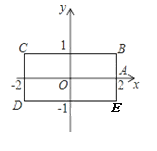
A. (-1,1) B. (1,-1) C. (-2,0) D. (-1,-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,是中心对称但不一定是轴对称图形的是( )
A.等边三角形
B.矩形
C.菱形
D.平行四边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形内角和等于1260°,则该多边形边数是( )
A. 8 B. 9 C. 10 D. 11
相关试题

