【题目】如图,矩形BCDE的各边分别平行于![]() 轴或
轴或![]() 轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2015次相遇地点的坐标
轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2015次相遇地点的坐标
是( )
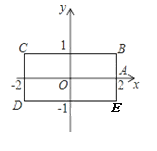
A. (-1,1) B. (1,-1) C. (-2,0) D. (-1,-1)
参考答案:
【答案】D
【解析】利用行程问题中的相遇问题,由于矩形的边长为4和2,物体乙是物体甲的速度的2倍,求得每次相遇的地点,找出规律即可解答.
解:矩形的边长为4和2,因为物体乙是物体甲的速度的2倍,时间相同,物体甲与物体乙的路程比为1:2,由题意知:
①第一次相遇物体甲与物体乙行的路程和为12×1,物体甲行的路程为12×![]() =4,物体乙行的路程为12×
=4,物体乙行的路程为12×![]() =8,在BC边相遇;
=8,在BC边相遇;
②第二次相遇物体甲与物体乙行的路程和为12×2,物体甲行的路程为12×2×![]() =8,物体乙行的路程为12×2×
=8,物体乙行的路程为12×2×![]() =16,在DE边相遇;
=16,在DE边相遇;
③第三次相遇物体甲与物体乙行的路程和为12×3,物体甲行的路程为12×3×![]() =12,物体乙行的路程为12×3×
=12,物体乙行的路程为12×3×![]() =24,在A点相遇…
=24,在A点相遇…
此时甲乙回到原出发点,则每相遇三次,两点回到出发点,
∵2015÷3=671…2,
故两个物体运动后的第2014次相遇地点的是:第二次相遇地点,
即物体甲行的路程为12×2×![]() =8,物体乙行的路程为12×2×
=8,物体乙行的路程为12×2×![]() =16,
=16,
此时相遇点的坐标为:(-1,-1),
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE.
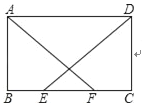
求证:(1)△ABF≌△DCE;
(2)四边形ABCD是矩形.
-
科目: 来源: 题型:
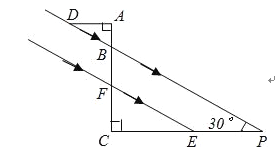
查看答案和解析>>【题目】如图,某一时刻太阳光从教室窗户射入室内,与地面的夹角∠BPC为30°,窗户的一部分在教室地面所形成的影长PE为3.5米,窗户的高度AF为2.5米.求窗外遮阳蓬外端一点D到教室窗户上椽的距离AD.(结果精确0.1米)
-
科目: 来源: 题型:
查看答案和解析>>【题目】小东从甲地出发匀速前往相距20km的乙地,一段时间后,小明从乙地出发沿同一条路匀速前往甲地.小东出发2.5h后,在距乙地7.5km处与小明相遇,之后两人同时到达终点.图中线段AB、CD分别表示小东、小明与乙地的距离y(km)与小东所用时间x(h)的关系.
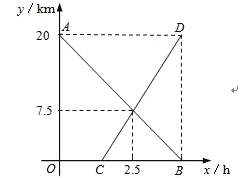
(1)求线段AB、CD所表示的y与x之间的函数表达式;
(2)小东出发多长时间后,两人相距16km?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,是中心对称但不一定是轴对称图形的是( )
A.等边三角形
B.矩形
C.菱形
D.平行四边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形内角和等于1260°,则该多边形边数是( )
A. 8 B. 9 C. 10 D. 11
-
科目: 来源: 题型:
查看答案和解析>>【题目】a2·a3等于()
A. a5 B. a6 C. a8 D. a9
相关试题

