【题目】阅读下列材料,并用相关的思想方法解决问题.
计算:(1﹣![]() ﹣
﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() +
+![]() +
+![]() )﹣(1﹣
)﹣(1﹣![]() ﹣
﹣![]() ﹣
﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() +
+![]() ).
).
令![]() +
+![]() +
+![]() =t,则
=t,则
原式=(1﹣t)(t+![]() )﹣(1﹣t﹣
)﹣(1﹣t﹣![]() )t
)t
=t+![]() ﹣t2﹣
﹣t2﹣![]() t﹣
t﹣![]() t+t2
t+t2
=![]()
问题:
(1)计算
(1﹣![]() ﹣
﹣![]() ﹣
﹣![]() ﹣…﹣
﹣…﹣![]() )×(
)×(![]() +
+![]() +
+![]() +
+![]() +…+
+…+![]() +
+![]() )﹣(1﹣
)﹣(1﹣![]() ﹣
﹣![]() ﹣
﹣![]() ﹣
﹣![]() ﹣…﹣
﹣…﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() +
+![]() +…+
+…+![]() );
);
(2)解方程(x2+5x+1)(x2+5x+7)=7.
参考答案:
【答案】
(1)
解:设![]() +
+![]() +…+
+…+![]() =t,
=t,
则原式=(1﹣t)×(t+![]() )﹣(1﹣t﹣
)﹣(1﹣t﹣![]() )×t
)×t
=t+![]() ﹣t2﹣
﹣t2﹣![]() t﹣t+t2+
t﹣t+t2+![]() t
t
=![]() ;
;
(2)
解:设x2+5x+1=t,
则原方程化为:t(t+6)=7,
t2+6t﹣7=0,
解得:t=﹣7或1,
当t=1时,x2+5x+1=1,
x2+5x=0,
x(x+5)=0,
x=0,x+5=0,
x1=0,x2=﹣5;
当t=﹣7时,x2+5x+1=﹣7,
x2+5x+8=0,
b2﹣4ac=52﹣4×1×8<0,
此时方程无解;
即原方程的解为:x1=0,x2=﹣5.
【解析】(1)设![]() +
+![]() +…+
+…+![]() =t,则原式=(1﹣t)×(t+
=t,则原式=(1﹣t)×(t+![]() )﹣(1﹣t﹣
)﹣(1﹣t﹣![]() )×t,进行计算即可;
)×t,进行计算即可;
(2)设x2+5x+1=t,则原方程化为:t(t+6)=7,求出t的值,再解一元二次方程即可.
【考点精析】利用换元法和有理数的四则混合运算对题目进行判断即可得到答案,需要熟知换元法是中学数学中的一个重要的数学思想,其应用非常广泛,当分式方程具有某种特殊形式,一般的去分母不易解决时,可考虑用换元法;在没有括号的不同级运算中,先算乘方再算乘除,最后算加减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了更好得节约能源,决定购买一批节省能源的10台新机器。现有甲、乙两种型号的设备,其中每台的价格、工作量如下表。经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台甲型设备比购买3台乙型设备少6万元.
甲型
乙型
价格(万元/台)


产量(吨/月)
240
180
(1)求a, b的值;
(2)经预算:该公司购买的节能设备的资金不超过110万元,请列式解答有几种购买方案可供选择;
(3)在(2)的条件下,若每月要求产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)3x﹣x﹣5x
(2)(8a﹣7b)﹣2(4a﹣5b)
-
科目: 来源: 题型:
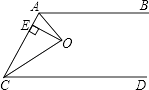
查看答案和解析>>【题目】如图,AB∥CD,O为∠BAC,∠ACD的平分线的交点,OE⊥AC于E,且OE=3,则AB与CD之间的距离为( )
A.3
B.3.5
C.4
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果将抛物线y=x2+2向下平移1个单位,那么所得新抛物线的表达式是( )
A.y=(x﹣1)2+2
B.y=(x+1)2+2
C.y=x2+1
D.y=x2+3 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:a3÷a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并解决相关的问题.
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为a1 , 依此类推,排在第n位的数称为第n项,记为an .
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0).如:数列1,3,9,27,…为等比数列,其中a1=1,公比为q=3.
(1)等比数列3,6,12,…的公比q为 ,第4项是
(2)如果一个数列a1 , a2 , a3 , a4 , …是等比数列,且公比为q,那么根据定义可得到: =q,
=q, =q,
=q, =q,…
=q,… =q.
=q.
所以:a2=a1q,a3=a2q=(a1q)q=a1q2 , a4=a3q=(a1q2)q=a1q3 , …
由此可得:an=(用a1和q的代数式表示).
(3)若一等比数列的公比q=2,第2项是10,请求它的第1项与第4项.
相关试题

