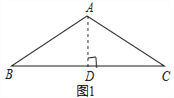
【题目】问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=![]() ∠BAC=60°,于是
∠BAC=60°,于是![]() ;
;
迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
(1)求证:△ADB≌△AEC;
(2)若AD=2,BD=3,请计算线段CD的长;
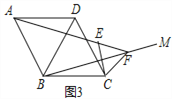
拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
(3)证明:△CEF是等边三角形;
(4)若AE=4,CE=1,求BF的长.

参考答案:
【答案】(1)见解析;(2)CD =![]() ;(3)见解析;(4)
;(3)见解析;(4)![]()
【解析】试题分析:迁移应用:(1)如图2中,只要证明∠DAB=∠CAE,即可根据SAS解决问题;
(2)结论:CD=![]() AD+BD.由△DAB≌△EAC,可知BD=CE,在Rt△ADH中,DH=ADcos30°=
AD+BD.由△DAB≌△EAC,可知BD=CE,在Rt△ADH中,DH=ADcos30°=![]() AD,由AD=AE,AH⊥DE,推出DH=HE,由CD=DE+EC=2DH+BD=
AD,由AD=AE,AH⊥DE,推出DH=HE,由CD=DE+EC=2DH+BD=![]() AD+BD,即可解决问题;
AD+BD,即可解决问题;
拓展延伸:(3)如图3中,作BH⊥AE于H,连接BE.由BC=BE=BD=BA,FE=FC,推出A、D、E、C四点共圆,推出∠ADC=∠AEC=120°,推出∠FEC=60°,推出△EFC是等边三角形;
(4)由AE=4,EC=EF=1,推出AH=HE=2,FH=3,在Rt△BHF中,由∠BFH=30°,可得![]() =cos30°,由此即可解决问题.
=cos30°,由此即可解决问题.
试题解析:
迁移应用:(1)证明:如图2,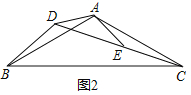
∵∠BAC=∠DAE=120°,
∴∠DAB=∠CAE,
在△DAE和△EAC中,
DA=EA,∠DAB=∠EAC,AB=AC,
∴△DAB≌△EAC,
(2)结论:CD=![]() AD+BD.
AD+BD.
理由:如图2-1中,作AH⊥CD于H.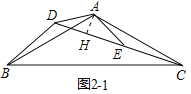
∵△DAB≌△EAC,
∴BD=CE,
在Rt△ADH中,DH=ADcos30°=![]() AD,
AD,
∵AD=AE,AH⊥DE,
∴DH=HE,
∵CD=DE+EC=2DH+BD=![]() AD+BD=
AD+BD=![]() .
.
拓展延伸:(3)如图3中,作BH⊥AE于H,连接BE.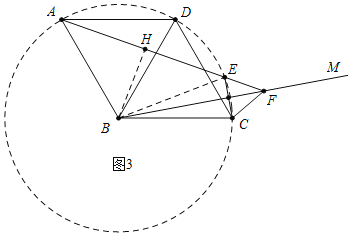
∵四边形ABCD是菱形,∠ABC=120°,
∴△ABD,△BDC是等边三角形,
∴BA=BD=BC,
∵E、C关于BM对称,
∴BC=BE=BD=BA,FE=FC,
∴A、D、E、C四点共圆,
∴∠ADC=∠AEC=120°,
∴∠FEC=60°,
∴△EFC是等边三角形,
(4)∵AE=4,EC=EF=1,
∴AH=HE=2,FH=3,
在Rt△BHF中,∵∠BFH=30°,
∴![]() =cos30°,
=cos30°,
∴BF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察理解,并解决问题.
问题情境:如图所示,用一些相同的小正方形,拼在一起,排成如下的一些大正方形:
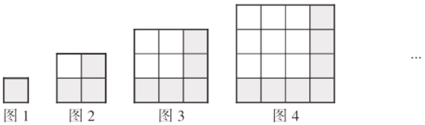
问题解决:(1)完成下表:
图序号
1
2
3
4
…
每一行小正方形的个数
1
2
3
______
…
______
阴影小正方形的个数
1
3
5
______
…
______
(2)根据图形规律推测:
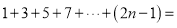 ______(用含
______(用含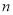 的代数式表示)
的代数式表示)(3)像(1),(2)这样,根据某类事物的部分对象具有的某种性质,推出这类事物的所有对象具有的这种性质的推理,叫做归纳推理.对于科学的发现,归纳推理是十分有用的,通过观察、实验,对有限个对象的性质作归纳整理,提出对某类事物带有规律性的猜测,是科学研究的基本方法.请观察下列等式的规律:第一个等式:
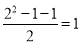 ;第二个等式:
;第二个等式: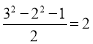 ;第三个等式:
;第三个等式: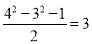 ;…猜想并直接写出第
;…猜想并直接写出第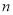 个等式.(用含
个等式.(用含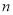 的代数式表示)
的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
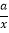 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.(1)求一次函数y=kx+b和y=
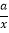 的表达式;
的表达式;(2)已知点C在x轴上,且△ABC的面积是8,求此时点C的坐标;
(3)反比例函数y=
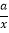 (1≤x≤4)的图象记为曲线C1,将C1向右平移3个单位长度,得曲线C2,则C1平移至C2处所扫过的面积是_________.(直接写出答案)
(1≤x≤4)的图象记为曲线C1,将C1向右平移3个单位长度,得曲线C2,则C1平移至C2处所扫过的面积是_________.(直接写出答案)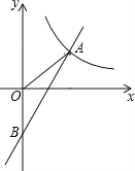
-
科目: 来源: 题型:
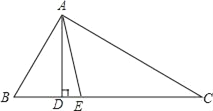
查看答案和解析>>【题目】如图,在△ABC中,∠B=60°,∠C=30°,AD和AE分别是△ABC的高和角平分线,求∠DAE的度数.
-
科目: 来源: 题型:
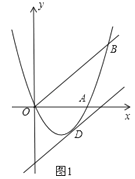
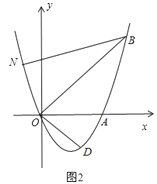
查看答案和解析>>【题目】如图1,已知抛物线y=ax2+bx(a≠0)经过A(6,0)、B(8,8)两点.
(1)求抛物线的解析式;
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标;
(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,在坐标平面内有点P,求出所有满足△POD∽△NOB的点P坐标(点P、O、D分别与点N、O、B对应).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,BA=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
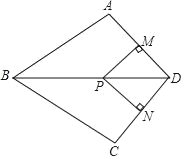
(1)求证:点A与C关于直线BD对称.
(2)若∠ADC=90°,求证四边形MPND为正方形.
相关试题

