【题目】观察理解,并解决问题.
问题情境:如图所示,用一些相同的小正方形,拼在一起,排成如下的一些大正方形:
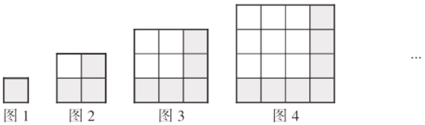
问题解决:(1)完成下表:
图序号 | 1 | 2 | 3 | 4 | … |
|
每一行小正方形的个数 | 1 | 2 | 3 | ______ | … | ______ |
阴影小正方形的个数 | 1 | 3 | 5 | ______ | … | ______ |
(2)根据图形规律推测:![]() ______(用含
______(用含![]() 的代数式表示)
的代数式表示)
(3)像(1),(2)这样,根据某类事物的部分对象具有的某种性质,推出这类事物的所有对象具有的这种性质的推理,叫做归纳推理.对于科学的发现,归纳推理是十分有用的,通过观察、实验,对有限个对象的性质作归纳整理,提出对某类事物带有规律性的猜测,是科学研究的基本方法.请观察下列等式的规律:第一个等式:![]() ;第二个等式:
;第二个等式:![]() ;第三个等式:
;第三个等式:![]() ;…猜想并直接写出第
;…猜想并直接写出第![]() 个等式.(用含
个等式.(用含![]() 的代数式表示)
的代数式表示)
参考答案:
【答案】(1)4,7,n,2n-1;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据图形可填写第4列,分析前4列的规律可填写第n列;
(2)根据有理数的加法法则计算即可;
(3)根据所给三个等式归纳出结论即可.
解:(1)
图序号 | 1 | 2 | 3 | 4 | … |
|
一边上小正方形的个数 | 1 | 2 | 3 | 4 | … |
|
阴影小正方形的个数 | 1 | 3 | 5 | 7 | … |
|
(2)![]()
=![]()
=![]()
=![]() ;
;
(3)∵第一个等式:![]() ;
;
第二个等式:![]() ;
;
第三个等式:![]() ;
;
…;
∴第![]() 个等式是:
个等式是:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外完全相同,其中红球有
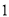 个,若从中随机摸出一个球,这个球是白球的概率为
个,若从中随机摸出一个球,这个球是白球的概率为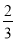 .
.(
 )请直接写出袋子中白球的个数.
)请直接写出袋子中白球的个数.(
 )随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个长方形运动场被分隔成
 、
、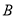 、
、 、
、 、
、 共
共 个区,
个区,  区是边长为
区是边长为 的正方形,
的正方形,  区是边长为
区是边长为 的正方形.
的正方形.(1)列式表示每个
 区长方形场地的周长,并将式子化简;
区长方形场地的周长,并将式子化简;(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果
 ,
,  ,求整个长方形运动场的面积.
,求整个长方形运动场的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
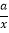 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.(1)求一次函数y=kx+b和y=
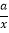 的表达式;
的表达式;(2)已知点C在x轴上,且△ABC的面积是8,求此时点C的坐标;
(3)反比例函数y=
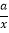 (1≤x≤4)的图象记为曲线C1,将C1向右平移3个单位长度,得曲线C2,则C1平移至C2处所扫过的面积是_________.(直接写出答案)
(1≤x≤4)的图象记为曲线C1,将C1向右平移3个单位长度,得曲线C2,则C1平移至C2处所扫过的面积是_________.(直接写出答案)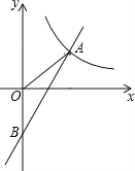
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=
 ∠BAC=60°,于是
∠BAC=60°,于是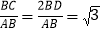 ;
;
迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
(1)求证:△ADB≌△AEC;
(2)若AD=2,BD=3,请计算线段CD的长;
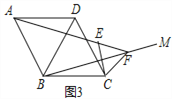
拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
(3)证明:△CEF是等边三角形;
(4)若AE=4,CE=1,求BF的长.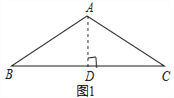

-
科目: 来源: 题型:
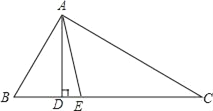
查看答案和解析>>【题目】如图,在△ABC中,∠B=60°,∠C=30°,AD和AE分别是△ABC的高和角平分线,求∠DAE的度数.
相关试题

