【题目】如图,点C是线段AB上除点A,B外的任意一点,分别以AC,BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.
(1)求证:BD=AE.
(2)求证:△NMC是等边三角形.

参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)先由△ACD和△BCE是等边三角形,可知AC=DC,CE=CB,∠DCA=60°,∠ECB=60°,故可得出∠DCA+∠DCE=∠ECB+∠DCE,即∠ACE=∠DCB,根据SAS定理可知△ACE≌△DCB,然后由全等三角形的性质即可得出结论;
(2)由(1)中△ACE≌△DCB,可知∠CAM=∠CDN,再根据∠ACD=∠ECB=60°,A、C、B三点共线可得出∠DCN=60°,由全等三角形的判定定理可知,△ACM≌△DCN,故MC=NC,再根据∠MCN=60°可知△MCN为等边三角形.
证明:(1)∵△ACD和△BCE是等边三角形,
∴AC=DC,CE=CB,∠DCA=60°,∠ECB=60°,
∵∠DCA=∠ECB=60°,
∴∠DCA+∠DCE=∠ECB+∠DCE,即∠ACE=∠DCB,
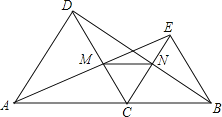
在△ACE与△DCB中,
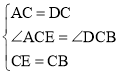 .
.
∴△ACE≌△DCB(SAS),
∴AE=BD;
(2)∵由(1)得,△ACE≌△DCB,
∴∠CAM=∠CDN,
∵∠ACD=∠ECB=60°,而A.C.B三点在同一条直线上,
∴∠DCN=60°,
在△ACM与△DCN中,
∵∠MAC=∠NDC,AC=DC,∠ACM=∠DCN=60°,
∴△ACM≌△DCN(ASA),
∴MC=NC,
∵∠MCN=60°,
∴△MCN为等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 经过点A(
经过点A( ,0),B(
,0),B( ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AB=4,点E为AB的中点.以AE为边作等边△ADE(点D与点C分别在AB的异侧),连接CD.则△ACD的面积为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2),点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当四边形CDBF的面积最大时,E点的坐标为_____.
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2),点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当四边形CDBF的面积最大时,E点的坐标为_____.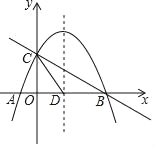
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D为△ABC内一点, ∠BAD=15°,AD=AC,CE⊥AD于E,且CE=5.
(1)求BC的长;
(2)求证:BD=CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(
 ,0),B(0,2),点B2019的坐标为_____
,0),B(0,2),点B2019的坐标为_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学校开展的数学活动课上,小明和小刚制作了一个正三楼锥(质量均匀,四个面完全相同),并在各个面上分别标记数字1,2,3,4,游戏规则如下每人投掷三棱锥两次,并记录底面的数字,如果两次所掷数字的和为单数,那么算小明赢,如果两欢所掷数字的和为偶数,那么算小明赢;
(1)请用列表或者面树状围的方法表示上述游戏中的所有可能结果.
(2)请分别隶出小明和小刚能赢的概率,并判新游戏的公平性.

相关试题

