【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=4,E为斜边AB的中点,点P是射线BC的一个动点,连接AP、PE,将△AEP沿着边PE叠,折叠后得到△EPA,当折叠后△EPA与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则BP的长__________
参考答案:
【答案】4或![]() .
.
【解析】分析: 根据30°角所对直角边等于斜边的一半可求出AB,即可得到AE的值,然后根据勾股定理求出BC,①若![]() 与AB交于点F,连接
与AB交于点F,连接![]() ,如图1,易得
,如图1,易得![]() ,即可得到
,即可得到![]() ,
,![]() .从而可得四边形
.从而可得四边形![]() 是平行四边形,即可得到
是平行四边形,即可得到![]() ,从而可求出BP;②若
,从而可求出BP;②若![]() 与BC交于点G,连接
与BC交于点G,连接![]() ,交EP与H,如图2,同理可得
,交EP与H,如图2,同理可得![]() ,
,![]() EG=
EG=![]() ,根据三角形中位线定理可得AP=4=AC,此时点P与点C重合
,根据三角形中位线定理可得AP=4=AC,此时点P与点C重合![]() ,从而可求出BP.
,从而可求出BP.
详解:因为Rt△ABC中,∠ACB=90°,∠A=60°,AC=4,E为斜边AB的中点,
所以AB=8,AE=4,BC=![]() ,
,
①若PA’与AB交于点F,连接A’B,如图1.
由折叠可得AE=AE’=4,.
因为点E是AB的中点,![]()
由题可得![]() ,
,![]() ,
,![]() ,
,![]()
所以四边形A’EPB是平行四边形,
所以BP=A’E=4;
②若EA’与BC交于点G,连接AA’,交EP与H,如图2. .
.
同理可得![]() ,
,
因为![]()
所以![]() ,
,
所以点P与点C重合,
所以BP=BC=![]() ,
,
故答案为4或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市从今年1月1日起调整居民用水价格,每立方米水费上涨
 ,小丽家去年12月的水费是15元,而今年7月的水费则是30元.已知小丽家今年7月的用水量比去年12月的用水量多5m3,求该市今年居民用水的价格.请表述出此题的主要等量关系,(写出一个即可)_____________.
,小丽家去年12月的水费是15元,而今年7月的水费则是30元.已知小丽家今年7月的用水量比去年12月的用水量多5m3,求该市今年居民用水的价格.请表述出此题的主要等量关系,(写出一个即可)_____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a<0,c>0)与x轴交于A,B两点,与y轴交于点C,其对称轴l为x=﹣1,直线y=kx+m经过A,C两点,与抛物线的对称轴l交于点D,且AD=2CD,连接BC,BD.
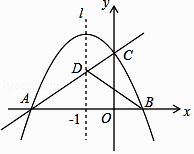
(1)求A,B两点的坐标;
(2)求证:a=﹣k;
(3)若△BCD是直角三角形,求抛物线的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】北京,上海两地的两个厂家同时生产同种型号的计算机,除本地使用外,北京可调运给外地10台,上海可调运给外地4台,现协议给武汉6台,重庆8台,每台的运费如下表所示,现有一种调运方案,预计的运费为7600元,这种调运方案中,北京,上海应分别调往武汉,重庆各多少台?

-
科目: 来源: 题型:
查看答案和解析>>【题目】列一元一次方程解应用题.
(1)商店出售茶壶和茶杯,茶壶每只定价20元,茶杯每只定价5元,该商品制定了两种优惠方法:
①买一只茶壶赠一只茶杯;②按总价的90%付款.某顾客购买茶壶5只,茶杯若干只(不少于5只),问顾客买多少只茶杯时,两种方法付款相同.假如该顾客买了茶杯20只,哪种买法实惠?
(2)某人原计划骑车以每小时12千米的速度由A地到B地,这样便可在规定的时间到达,但他因事将原计划出发的时间推迟了20分钟,只好以每小时15千米的速度前进,结果比规定时间早4分钟到达B地,求A,B两地间的距离.
(3)某工厂完成一批产品,一车间单独完成需30天,二车间单独完成需20天.
①如一车间先做若干天,然后由二车间继续做,直至完成,前后共做了25天,问一车间先做了几天?
②如一车间先做了3天后,二车间加入一起做,还需多少天才能完成?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B是平面上的两定点,在平面上找一点C,使△ABC为等腰直角三角形,且点C为直角顶点,这样的点C有几个?请用尺规作图确定点C的位置,保留作图迹并说明理由

-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习一元一次不等式与一次函数中,小明在同一个坐标系中分别做出了一次函数l1和l2的图像,l1与坐标轴的交点分别为点A、点B,l1与l2的交点为点C,但被同桌小英不小心用墨水给部分污染了,我们一起来探讨
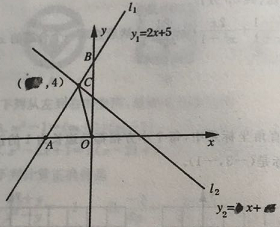
(1)写出点A、点C的坐标:A(①,0);C(②,4);
(2)求△BOC的面积:S△BOC=③
(3)直接写出不等式2x+5<·x+·的解集并回答下面问题
在解决问题(3)时,小明和小英各抒己见.小明:“l2的表达式中已经看不清楚了,并且只知道l2上一个点C的坐标,求不出该直线的表达式,所以无法求出该不等式的解集”小英说:“不用求出l2的表达式就可以得出该不等式的解集.”你同意谁的说法?并说明理由
相关试题

